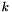All lattices considered are integral lattices in $\mathbb{Z}^n$ , given by a generating system $b_1, \ldots, b_k$ . Note that $k$ can be in any relation to 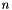$n$ since we do not assume that $b_1, \ldots, b_k$ forms a basis of the lattice.

Introduction to lattice reduction

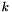Let $b_1, \ldots, b_k$ be $k$ linearly independent vectors in 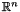$\mathbb{R}^n$ , where 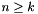$n \ge k$ . Then the lattice of rank $k$ generated by $b_1, \ldots, b_k$ is the subgroup

$\Lambda(b_1, \ldots, b_k) := \biggl\{ \sum_{i=1}^k \lambda_i b_i \;\biggm|\; \lambda_1, \dots, \lambda_k \in \mathbb{Z} \biggr\} \subseteq \mathbb{R}^n.$

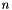Any subgroup of $\mathbb{R}^n$ of this form is called a lattice, and the corresponding number $k$ its rank. The dimension $n$ of the ambient space is called the dimension of the lattice, and the vectors $b_1, \ldots, b_k$ are called a basis of the lattice. In case the lattice is contained in $\mathbb{Z}^n$ , we say that the lattice is integral.

An example for a two-dimensional lattice of rank 2 is given in the following picture:

A two-dimensional lattice

This lattice can be given implicitly as

$\Lambda = \{ (x, y) \in \mathbb{Z}^2 \mid x + y \equiv 0 \pmod{2} \}$

The large dot in the center represents the zero vector. This lattice can be generated in different ways. A simple basis is

$b_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix}, \quad b_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix},$

which is shown in the following picture:

A simple basis of the above lattice

But also other bases are possible. In fact, as soon as 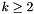$k \ge 2$ , there are infinitely many bases for every lattice of rank 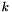$k$ . The following picture shows a more complicated basis of the same lattice as before:

A more complicated basis of the above lattice

The aim of lattice reduction is to start with a (complicated) basis and try to find a better, "nicer" basis. One goal is to find as short as possible basis vectors. The vectors in the first basis 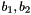$b_1, b_2$ are a relatively good choice, but not optimal: a better basis would be

$c_1 = \begin{pmatrix} 1 \\ -1 \end{pmatrix}, \quad c_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix},$

as demonstrated by the following picture:

An 'optimal' basis for the above lattice

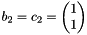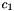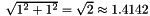Note that both in this basis as in the first one, a shortest non-zero vector is part of the basis, namely $b_2 = c_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix}$ and also $c_1$ in the last basis: their Euclidean length is $\sqrt{1^2 + 1^2} = \sqrt{2} \approx 1.4142$ .

Since finding such shortest vectors is hard (for 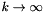$k \to \infty$ ), as M. Ajtai showed in 1998 [1], most lattice basis reduction algorithms try to find good approximations of a shortest vector, where the approximation quality usually increases with running time, but is often far away from optimal. The first polynomial time lattice basis reduction algorithm, 1982's celebrated LLL algorithm [9], has a exponential approximation bound (which Schnorr showed is optimal). For some problems, such bounds already suffice, while for others, better approximations are needed. Since 1982, many new algorithms have been designed to find better approximations. The plll library tries to make many of them available.

For a more detailed description of lattice reduction algorithms, see Lattice Reduction.

Usage

A simple example of how to use the plll library is the following:

#include <plll.hpp>
#include <iostream>
int main()
{
    plll::linalg::math_matrix<plll::arithmetic::Integer> A;
    std::cin >> A;
    
    plll::LatticeReduction lr;
    lr.setLattice(A);
    lr.lll();
    
    std::cout << lr.getLattice() << "\n";
}

It applies LLL with standard parameters (that is, reduction parameter 0.99) to a basis read from standard input, and writes the resulting basis to standard output.

A more thorough discussion of this example can be found in A simple example. More examples can be found in Examples. For a detailed explanation of the interface of the plll::LatticeReduction class, see its description. For a detailed description of how to work with matrices, including how to input and output them, see Matrices and Vectors. To know more about how to work with the arithmetic functions provided by plll, see Arithmetic Contexts. And for a detailed description of the supported lattice reduction algorithms, see Supported algorithms.

Attributions

All code except the memory allocator was written by Felix Fontein.

All algorithms implemented in this library are taken from published papes. Some were slightly modified. See Supported algorithms for descriptions of the algorithms, attributions to their inventors and references to the relevant publications.

The memory allocator in the files plll/src/utilities/dlalloc.c and plll/src/utilities/dlalloc.h is Doug Lea's dlmalloc, which was released to the public domain. For more information, check out plll/src/utilities/dlalloc.c or ftp://gee.cs.oswego.edu/pub/misc/malloc.c.

License

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.