Note that most features are implemented in the plll command line program, which can be found in tools/src/plll.cpp. Therefore, to see how a certain feature is used which is not presented in this section, you can always check out tools/src/plll.cpp.

A simple example

This is the same sample as in Usage. It can be found in examples/src/example-01.cpp:

#include <plll.hpp>
#include <iostream>
int main()
{
    plll::linalg::math_matrix<plll::arithmetic::Integer> A;
    std::cin >> A;
    
    plll::LatticeReduction lr;
    lr.setLattice(A);
    lr.lll();
    
    std::cout << lr.getLattice() << "\n";
}

The example first creates an empty (i.e. 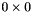$0 \times 0$ ) matrix with arbitrary precision integer entries, called A, and then reads a matrix from standard input (std::cin) and stores the result in A.

Then, an instance called lr of the lattice reduction class is created. It is initialized with the lattice generated by the rows of the matrix A. By calling lr.lll(), the Classic LLL algorithm is applied to this lattice basis with the default parameter 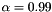$\alpha = 0.99$ .

Finally, the program reads the reduced lattice basis by lr.getLattice()—the result is a matrix whose rows yield the basis—and writes the matrix to standard output (std::cout).

To demonstrate how this example works on real-world data, let us consider the lattice in Introduction to lattice reduction. The first basis given there is

$b_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix}, \quad b_2 = \begin{pmatrix} 1 \\ 1 \end{pmatrix},$

, resulting in the following picture:

The input basis

To apply the program to this basis, we have to construct a matrix containing these vectors as its rows:

$A = \begin{pmatrix} 3 & 1 \\ 1 & 1 \end{pmatrix}$

To enter this matrix into our program, we have to write it as follows: [[3, 1], [1, 1]]

If we enter this at the beginning of our program, we get the following output:

[[3, 1], [1, 1]]
mat<2,2>[[1, 1], [1, -1]]

(The first line is the echo of the input.) Thus, as the output, we obtain the nice lattice basis in Introduction to lattice reduction, which yields the following picture:

The 'optimal' output basis

Finding a very short vector

While finding a shortest vector is NP hard [1], it is possible to approximate a short vector by using lattice reduction algorithms. An algorithm very helpful in practice is the Schnorr-Euchner BKZ algorithm. Unfortunately, in particular for higher block sizes, the algorithm often already obtained the shortest vector it will return long before it terminates. For that reason, it is wishful to be able to always see what is the shortest vector found so far. plll provides a callback hook for this reason which is called when the reduction algorithm stumbles over a vector with Euclidean norm shorter than any vector it encountered before while processing the current basis (

See also: desc-genconf-callback).

The following example shows how to do this in practice. It can be found in examples/src/example-02.cpp:

#include <plll.hpp>
#include <iostream>
void printShortestVector(const plll::linalg::math_matrix<plll::arithmetic::Integer> & A, 
                         unsigned index, const plll::arithmetic::Integer & sqnorm)
{
    std::cout << "The currently shortest vector is " << A.row(index) 
              << " with squared norm " << sqnorm << " (Integer)\n";
}
void printShortestVector_LI(const plll::linalg::math_matrix<plll::arithmetic::NInt<long> > & A, 
                            unsigned index, const plll::arithmetic::NInt<long> & sqnorm)
{
    std::cout << "The currently shortest vector is " << A.row(index) 
              << " with squared norm " << sqnorm << " (NInt<long>)\n";
}
int main()
{
    plll::linalg::math_matrix<plll::arithmetic::Integer> A;
    std::cin >> A;
    
    plll::LatticeReduction lr;
    lr.setLattice(A);
    lr.setMinCallbackFunction(printShortestVector, printShortestVector_LI);
    lr.bkz(0.99, 40);
}

It is similar to the previous example (A simple example), with the main differences that:

it does not output the resulting basis;
it does not use Classic LLL, but Schnorr-Euchner BKZ (with 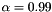$\alpha = 0.99$ and a blocksize of 40);
it sets a minimal vector callback function using plll::LatticeReduction::setMinCallbackFunction.

For the latter, it provides two functions: one for arbitrary precision integers (plll::arithmetic::Integer) and one for CPU integers (plll::arithmetic::NInt<long>). Since by default, plll determines which integer arithmetic to use on the fly (

See also: desc-genconf-arith), it is useful to provide both alternatives so that plll is not forced to convert the internal representation from one format to the other to be able to call the callback function.

To illustrate how this example works, let us use the SVP challenge basis for dimension 50 (with seed 0); it can be found here. By starting the program and pasting the basis' textual representation into it (or by using pipes or redirecting standard input), we let the program process this lattice basis.

The library internally first applies LLL, which converts this basis (given in Hermite Normal Form) into something more compact. The first output line is

The currently shortest vector is mat<1,50>[[-9770253083323343916965275912883206062922561406584472239
11084680829795919819354762585959322324750268253379484023871452642838548115289419328942293214818, 1, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]] with squared norm 954578453121893086923031172722240141
5470291413191066642863537393601930079752899447459843620501562783729668907328211198000701122696066760
0771389257710458775685171721625238187868083121323492585428385068254902186858647242938612587927038568
6748545805753278169971353652684403255259051086907300041494773125 (Integer)

(line breaks inserted for readability), which equals the second basis vector reduced by a multiple of the first basis vector. The squared norm here is quite large. At some point, plll decides to switch from arbitrary precision arithmetic to using CPU integers. This happens at this point:

The currently shortest vector is mat<1,50>[[-541, 416, 284, 24, 233, 164, -150, 71, -367, -288, -170,
71, -49, 125, 260, 143, -168, -30, 465, 49, 418, -349, -309, 134, 468, 109, -195, -218, -96, -104, 
-153, -608, -193, 657, 43, -155, -275, -234, -58, 896, -917, -23, 328, 356, 570, 155, 47, -606, -1,
0]] with squared norm 5626057
Changing lattice reduction interface.
(starting 4 threads)
The currently shortest vector is mat<1,50>[[364, 142, 213, 304, 786, -923, -71, 123, -7, -81, 323,
-436, 63, 209, 344, 279, 10, -287, -324, 267, -17, 327, -901, 239, 328, 190, 92, 664, 348, -254, -5,
340, -833, -157, -477, 561, -82, -41, 203, 271, 612, -458, -130, -26, 383, 16, -252, -75, 0, 0]] with
squared norm 6656166 (NInt<long>)

The vector returned before restarting the algorithm with CPU integer arithmetic already found a vector of Euclidean norm close to 2372, which is much less than the input vectors' norms. After restarting, the algorithm starts again with tracking shortest vectors, and thus first reports something much longer, namely a vector of Euclidean norm close to 2580. But shortly after that, it already finds a vector of Euclidean norm close to 2220, which beats the previously found shortest vector. Finally, it stops with a vector of Euclidean norm close to 1893:

The currently shortest vector is mat<1,50>[[-13, -124, -146, 277, -107, -180, 673, -311, -167, 47,
200, 395, 167, -25, -136, -392, 117, -165, 147, -515, 185, 637, 343, 8, 247, 44, -220, -146, 52, 135,
-347, -369, -332, -102, 469, -285, 1, 167, 397, 84, -97, -138, -135, 218, 567, 141, 72, 21, 312,
-41]] with squared norm 3584092 (NInt<long>)

It turns out that the shortest vectors in this lattice also have Euclidean norm close to 1893 (see the hall of fame for the SVP challenges), whence we can be quite sure that this is one of the shortest vectors. To verify this ourselves, we would have to do enumeration, which can be done via calling plll::LatticeReduction::svp.

Note that in particular in higher dimensions, the last output will come a long time before the algorithm terminates. Thus for an application where you need a short enough vector, and given a vector you can decide on the fly whether it was short enough, you could use this callback mechanism to perform this computation for every new shortest vector found. Note that from the callback functions, you can interrupt computation by throwing an exception of type plll::LatticeReduction::stop_reduction. If this exception isn't thrown, the reduction will continue until the reduction algorithm terminates.