plll  1.0
Matrices and Vectors

Introduction

The matrix and vector library of plll supplies flexible matrix and vector types which can be used with any types, and which are efficient when used with Arithmetic Contexts.

Similarly to the C++ template library Eigen, its aim is to provide efficient arithmetic while allowing to write operations in a natural way. For example, writing v = a + b + c for vectors v, a, b and c should be as efficient as directly writing 

for (unsigned i = 0; i < v.size(); ++i)
    v[i] = a[i] + b[i] + c[i];

This is achieved using template meta programming.

The Basic Templates

The most basic template is the plll::linalg::base_matrix<> template, which can describe matrices and vectors of any kind. In fact, all other templates are more or less typedefs (or wrappers, as templated typedefs are not available in C++98 and C++03) build on plll::linalg::base_matrix<>.

The plll::linalg::base_matrix<> template accepts up to five template parameters: 

 template<typename T,
          int Rows = plll::linalg::Flexible,
          int Cols = plll::linalg::Flexible,
          typename StorageTraits = plll::linalg::storage_traits<T>,
          bool MathObject = false>
 class plll::linalg::base_matrix;

The first template parameter, T, specifies the coefficient type. The next two template parameters, Rows and Cols, specify whether the number of rows and columns of the matrix are already determined on compile-time – in that case, they can be provided here by a non-negative integer – or whether they are flexible and can be chosen and changed during runtime – in that case, use plll::linalg::Flexible.

The fourth template parameter, StorageTraits, allows to modify the default storage behavior. By default, memory is allocated on the heap using the default allocator, but with a different StorageTraits class, one could also use a custom allocator, or store the data somewhere else. For more information on how such a StorageTraits object works, see the example implementations in matrix-mem.hpp.

The fifth (and last) template parameter, MathObject, allows to enable or disable "math mode". Only matrices with MathObject set to true can be added, subtracted or multiplied. Also, if MathObject is set to true, the library assumes that a function void setZero(T &) is avaiable for type T to set instances of type T to the value zero.

The following templates are more or less specializations of plll::linalg::base_matrix<>:

  • The template 

    template<typename T, int Rows = Flexible, int Cols = Flexible, typename StorageTraits = storage_traits<T> >
class plll::linalg::math_matrix

    is a short form for plll::linalg::base_matrix<T, Rows, Cols, StorageTraits, true>.

  • The template 

    template<typename T, int Cols = Flexible, typename StorageTraits = storage_traits<T>, bool MathObject = false>
class plll::linalg::base_rowvector

    is a short form for plll::linalg::base_matrix<T, 1, Cols, StorageTraits, MathObject>.

  • The template 

    template<typename T, int Rows = Flexible, typename StorageTraits = storage_traits<T>, bool MathObject = false>
class plll::linalg::base_colvector

    is a short form for plll::linalg::base_matrix<T, Rows, 1, StorageTraits, MathObject>.

  • The template 

    template<typename T, int Cols = Flexible, typename StorageTraits = storage_traits<T> >
class plll::linalg::math_rowvector

    is a short form for plll::linalg::base_rowvector<T, Cols, StorageTraits, true>.

  • The template 

    template<typename T, int Rows = Flexible, typename StorageTraits = storage_traits<T> >
class plll::linalg::math_colvector

    is a short form for plll::linalg::base_colvector<T, Rows, StorageTraits, true>.

The templates plll::linalg::math_matrix<>, plll::linalg::math_rowvector<> and plll::linalg::math_colvector<> provide math objects, while the templates plll::linalg::base_matrix<>, plll::linalg::base_rowvector<> and plll::linalg::base_colvector<> provide by default non-math objects.

Warning
Note that when compiled in C++98/03 mode, these "aliases" are in fact derived template classes. Therefore, if a function requires a plll::linalg::math_rowvector<> and something else is passed which should be of the same form (for example of type plll::linalg::base_rowvector<T, Cols, StorageTraits, true>), a plll::linalg::math_rowvector<T, Cols, StorageTraits> temporary object will be copy-constructed from the given one and will be used as the argument.

When compiled in C++11 mode, both types are identical and no temporary creation and copy construction is necessary.

Constructors

  • Create an empty matrix with each dimension being either zero, or the (at compile time) pre-determined dimension. All coefficients will be default constructed.
  • Create a copy of the given matrix or matrix expression.
    • plll::linalg::base_matrix::base_matrix(const base_matrix<T, Rows, Cols, StorageTraits, MathObject> &)
    • template<int Rs, int Cs, bool MO> plll::linalg::base_matrix::base_matrix(const base_matrix<T, Rs, Cs, StorageTraits, MO> &)
    • template<typename S, int Rs, int Cs, typename ST, bool MO> plll::linalg::base_matrix::base_matrix(const base_matrix<S, Rs, Cs, ST, MO> &)
    • template<typename MatrixType> plll::linalg::base_matrix::base_matrix(const MatrixType &)
    • template<template<typename> class Op, typename Data> plll::linalg::base_matrix::base_matrix<T, Rows, Cols, StorageTraits, MathObject> & operator = (const implementation::expressions::expr<Op, Data> &)
  • Create a vector with the given number of entries. These constructors are only avaiable if at least one of the dimensions was fixed at compile time to 1. The entries are default-constructed.
  • Create a vector with the given number of entries. These constructors are only avaiable if at least one of the dimensions was fixed at compile time to 1. The entries are copy-constructed from the given initializer object.
    • template<typename S, bool def> plll::linalg::base_matrix::base_matrix(size_type, const implementation::Initialize_Impl<S, def> &)
  • Create a matrix with the given number of rows and columns. The entries are default-constructed.
  • Create a matrix with the given number of rows and columns. The entries are copy-constructed from the given initializer object.
    • template<typename S, bool def> plll::linalg::base_matrix::base_matrix(size_type rows, size_type cols, const implementation::Initialize_Impl<S, def> &)

Note that an initializer object obj can be specified by writing plll::linalg::Initialize(obj). A default constructed object of type S is given by plll::linalg::Initialize<S>().

Note that also the vector templates plll::linalg::base_rowvector<>, plll::linalg::base_colvector<>, plll::linalg::math_rowvector<> and plll::linalg::math_colvector<> provide all of the above listed constructors as well.

Operations

General Operations

The following global operations are available for all vectors and matrices:

  • void plll::linalg::swap(MatrixTypeA & A, MatrixTypeB & B): swaps the contents of matrices A and B, if compile time dimension specifiers do not obstruct this and if the coefficient types can be swapped.
  • void plll::linalg::assign(MatrixTypeA & A, const MatrixTypeB & B): copies the content of B into the matrix A. Note that A is resized if necessary. Requires that the coefficient type of MatrixTypeB can be implicitly converted to the coefficient type of MatrixTypeB.

  • void plll::linalg::transpose(MatrixTypeA & A, const MatrixTypeB & B): copies the transposed content of B into the matrix A. Note that A is resized if necessary. Requires that the coefficient type of MatrixTypeB can be implicitly converted to the coefficient type of MatrixTypeB.

    Note that currently, transposing a matrix via plll::linalg::transpose(A, A) is not allowed and will result in undefined behavior. Most likely, half of the entries of the matrix are lost, and the other half duplicated.

  • Comparisons using operator == and operator != are available for all matrices having coefficent types which can be tested for equality or inequality. These operators test whether the matrices have the same format and, if that is the case, whether the entries compare to be equal.

  • Comparisons using operator <, operator >, operator <= and operator >= are available for all matrices having coefficent types which can be tested for equality or inequality.

    For these comparison operators, a lexicographic approach is used. First, the size of the matrices are lexicographically compared: if the first matrix has 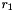$r_1$ rows and 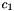$c_1$ columns and the second matrix has 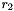$r_2$ rows and 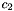$c_2$ columns, then we obtain the result

    \[\begin{cases} r_1 < r_2: & \text{first matrix is smaller} \\ r_1 = r_2 \wedge c_1 < c_2: & \text{first matrix is smaller} \\ c_1 = r_2 \wedge c_1 = c_2: & \text{content has to be checked} \\ r_1 = r_2 \wedge c_1 > c_2: & \text{first matrix is larger} \\ r_1 > r_2: & \text{first matrix is larger} \\ \end{cases}\]

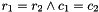    . In case $r_1 = r_2 \wedge c_1 = c_2$, i.e. when the matrices are of the same format, the content is checked as follows. If the first matrix is

    \[\begin{pmatrix} a_{11} & a_{12} & \dots \\ a_{21} & a_{22} & \dots \\ \vdots & \vdots & \ddots \end{pmatrix}\]

    and the second

    \[\begin{pmatrix} b_{11} & b_{12} & \dots \\ b_{21} & b_{22} & \dots \\ \vdots & \vdots & \ddots \end{pmatrix},\]

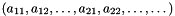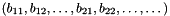    then the vectors $(a_{11}, a_{12}, \dots, a_{21}, a_{22}, \dots, \dots)$ and $(b_{11}, b_{12}, \dots, b_{21}, b_{22}, \dots, \dots)$ are compared lexicographically.

Math Operations

The following global operations are avaiable for math matrices and vectors:

  • Computing the sum 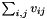$\sum_{i,j} v_{ij}$ of all entries 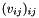$(v_{ij})_{ij}$ of $A$:
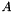    • template<typename RetType> void sum(RetType & result, const MatrixTypeA & A)
    • CoefficientType sum(const MatrixTypeA & A)
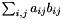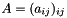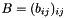  • Computing the dot product $\sum_{i,j} a_{ij} b_{ij}$ of $A = (a_{ij})_{ij}$ and $B = (b_{ij})_{ij}$:
    • template<typename RetType> void dot(RetType & result, const MatrixTypeA & A, const MatrixTypeB & B)
    • CoefficientType dot(const MatrixTypeA & A, const MatrixTypeB & B)
  • Computing the squared norm 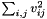$\sum_{i,j} v_{ij}^2$ of all entries 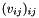$(v_{ij})_{ij}$ of $A$:
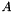    • template<typename RetType> void normSq(RetType & result, const MatrixTypeA & A)
    • CoefficientType normSq(const MatrixTypeA & A)
  • Addition of matrices:
    • add(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B)
    • ResultType operator + (const MatrixTypeA & A, const MatrixTypeB & B)
    • MatrixTypeA & operator += (MatrixTypeA & A, const MatrixTypeB & B)
  • Subtraction:
    • sub(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B)
    • ResultType operator - (const MatrixTypeA & A, const MatrixTypeB & B)
    • MatrixTypeA & operator -= (MatrixTypeA & A, const MatrixTypeB & B)
  • Negation:
    • neg(ResultType &, const MatrixTypeA & A)
    • ResultType operator - (const MatrixTypeA & A)
  • Multiplication:
    • mul(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B): Note that there, A or B can also be scalars.
    • ResultType operator * (const MatrixTypeA & A, const MatrixTypeB & B): Note that there, A or B can also be scalars.
    • MatrixTypeA & operator *= (MatrixTypeA & A, const MatrixTypeB & B): Note that there, B can also be a scalar.
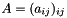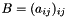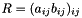  • Componentwise multiplication, i.e. given matrices $A = (a_{ij})_{ij}$ and $B = (a_{ij})_{ij}$, computes the matrix $R = (a_{ij} b_{ij})_{ij}$:
    • void componentwise_mul(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B)
    • ResultType componentwise_mul(const MatrixTypeA & A, const MatrixTypeB & B)
  • Combined addition/subtraction and multiplication:
    • void addmul(MatrixTypeR & R, const MatrixTypeA & A, const MatrixTypeB & B): adds the result of A * B to R. Note that there, A or B can also be scalars.
    • void submul(MatrixTypeR & R, const MatrixTypeA & A, const MatrixTypeB & B): subtracts the result of A * B from R. Note that there, A or B can also be scalars.
  • Division:
    • div(ResultType &, const MatrixTypeA & A, const ScalarTypeB & B)
    • ResultType operator * (const MatrixTypeA & A, const ScalarTypeB & B)
    • MatrixTypeA & operator *= (MatrixTypeA & A, const ScalarTypeB & B)
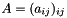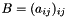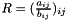  • Componentwise division, i.e. given matrices $A = (a_{ij})_{ij}$ and $B = (a_{ij})_{ij}$, computes the matrix $R = (\frac{a_{ij}}{b_{ij}})_{ij}$:
    • void componentwise_div(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B)
    • ResultType componentwise_div(const MatrixTypeA & A, const MatrixTypeB & B)
  • Modulo:
    • mod(ResultType &, const MatrixTypeA & A, const ScalarTypeB & B)
    • ResultType operator % (const MatrixTypeA & A, const ScalarTypeB & B)
    • MatrixTypeA & operator %= (MatrixTypeA & A, const ScalarTypeB & B)
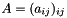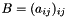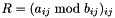  • Componentwise modulo, i.e. given matrices $A = (a_{ij})_{ij}$ and $B = (a_{ij})_{ij}$, computes the matrix $R = (a_{ij} \bmod b_{ij})_{ij}$:
    • void componentwise_mod(ResultType &, const MatrixTypeA & A, const MatrixTypeB & B)
    • ResultType componentwise_mod(const MatrixTypeA & A, const MatrixTypeB & B)

Input and Output

The usual ways of reading and writing objects in C++ are also provided for matrices and vectors. Namely, one can read them from an input stream using operator >>, and write them to an output stream using operator <<. Errors are reported by setting the stream's std::ios_base::badbit flag.

The output formats are:

  • mat<2, 3>[[1, 2, 3], [4, 5, 6]]: the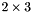 $2 \times 3$ matrix $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$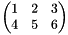
  • vec<3>[1, 2, 3]: the column vector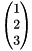 $\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$

In case the given matrix has precisely one column (determined at compile time), the second format is used. If this is not the case, always the first format is used.

To input matrices and vectors, they can be provided in both the above formats, as well as the following format:

  • [[1, 2, 3], [4, 5, 6]]: the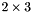 $2 \times 3$ matrix $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$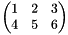

This allows to exchange information with other libraries such as NTL and fplll, which can read and write matrices in this format. Note that also the SVP challenge matrices are given in this format.

To allow more options while reading or writing matrices, the following functions are provided:

  • void print_matrix(std::ostream &, const MatrixType & mat, bool forceGeneric = false): prints the matrix mat on the given output stream. In case forceGeneric is true, the output will always be of the form mat<Rows, Cols>[...], while in case forceGeneric is false, column vectors will be printed as vec<Rows>[...].
  • bool scan_matrix(std::istream &, MatrixType & mat): reads the matrix mat from the input stream. In case of errors, returns false. Elements are created by first default-constructing them, and then using their operator >> to read their value in.
  • bool scan_matrix(std::istream &, MatrixType & mat, const S & default_object): reads the matrix mat from the input stream. In case of errors, returns false. Elements are created by first copy-constructing them from default_object, and then using their operator >> to read their value in. Note that default_object could be a context object as described in Contexts to create entries of a given precision.