Introduction
With aritrary precision floating point types, the main problem is how to store the default precision for new variables. Low-level libraries such as MPFR, but also high level libraries such as NTL, use a global (static) variable to store the precision, while allowing to change the precision of variables during initalization (MPFR) or later (MPFR and NTL).
In the context of multithreading, using one global variable for all threads is not acceptable. Thus, one has to carry around the required precision per thread (or logical part of the program), and initialize floating point variables using this precision. On the other hand, for fixed precision floating point types such as the native float, double and long double, such a precision is not needed.
The idea in the plll library is to carry around contextes, which are lightweight objects containing no (for native types) or very little (for arbitrary precision floating point types) information which are used to initialize new variables in a uniform way: if c is an instance of a context type Context, then a variable v of type Context::Type is initialized via
with the correct precision given by c in the case it carries a precision, or c is ignored in case of native types or arbitrary precision integer types. For other types later added, a context could in theory also hold other information; code written using contexts should be agnostic about this extra information.
Contexts
The basic information captured by every context is a typedef Type, which yields the type described by this context, together with an enum providing certain properties:
is_cputype:truefor native types supported by CPU (or emulated natively on CPUs, such aslong doubleon most UltraSPARC CPUs).is_realtype:truefor types representing (most or all) rational numbers, such as floating point types.is_inttype:truefor types representing (a range of or all) integer types. Only signed integer types are allowed.is_exact:truefor types which do use approximations (like floating point types). For example, for GMP and CPU integers, this is alwaystrue.has_infinity:truefor types having objects representing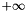 and
and 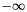 .
.has_uniform_rng:trueif the type provides a uniform random number generator. Such a context exhibits a typeUniformRNG, whose interface will be described in more detail below in Uniform Random Number Generator. Note that the rational number context fromrational.hppis an example of a context not providing a uniform random number generator.
Integer types also have a typedef Integer, being the same as Type. Besides the properties listed above, they also provide:
is_modulo:truefor types which are "wrap around", such as native integer arithmetic which in fact computes in rings such as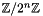 .
.
Real types also have a typedef Real, being the same as Type. Besides the properties listed above, they also provide:
is_variable_precision:trueif the precision of the current type can be modified. (See below for the interface.)has_squareroot:trueif (approximated) square roots are supported. This will befalsefor rational numbers, buttruefor most (or even all) floating point types. For more information, see Square Roots and Full Powers.has_full_power:trueif elements can be raised to fractional powers (where the powers are coming from the same context). This will befalsefor rational numbers, buttruefor most (or even all) floating point types. For more information, see Square Roots and Full Powers.has_special_fns:trueif special functions such aslgammaetc. are supported for this type. A list of special functions with explanations can be found below in Special Functions.has_huge_exponent:truefor floating point types using at least the range of asigned intfor the exponent. If the exponent range is (much) smaller, this has to be set tofalse.has_constants:trueif special constants such as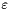 ,
, 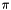 ,
, 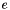 and
and 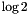 are provided by the context. See below in Constants for more information.
are provided by the context. See below in Constants for more information.has_trigonometric:trueif trigonometric functions such assinandcosare provided. See below in Trigonometric Functions for more information.
Integer contexts do not provide any functions. Real contexts, on the other hand, provide a few standard functions:
void setRealPrecision(unsigned long): sets the precision of the context to (at least) the given value, if possible. If this is not possible, the context is free should chose a precision as high as possible. In case the precision cannot be changed (i.e.is_variable_precisionisfalse), this call can be ignored.unsigned long getRealPrecision() const: retrieves the current precision of the context. For types not having a precision, the return value should be a large number such asstd::numeric_limits<unsigned long>::max().unsigned long getMinRealPrecision() const: retrieves the minimal possible precision. For types not having a precision, the return value should be a large number such asstd::numeric_limits<unsigned long>::max().unsigned long getMaxRealPrecision() const: retrieves the maximal possible precision. For types not having a precision, the return value should be a large number such asstd::numeric_limits<unsigned long>::max(). In any case, the value returned must always be larger than the one returned bygetMinRealPrecision().
Operands
Context types are expected to overload any reasonable operator, such as the arithmetic operators +, -, *, /, %, <<, >>, ++, --, the arithmetic assignment operators +=, -=, *=, /=, %=, <<=, >>=, and the comparison operators ==, !=, <, >, <=, >=.
Additionally, excepted some operator-like functions:
Context::Type abs(const Context::Type &): takes the absolute value of the operand and returns the result.Context::Type square(const Context::Type &): squares the operand and returns the result.
For real types, there are variants which also accept a context:
Context::Type abs(const Context::Type &, const Context &): takes the absolute value of the first operand and returns the result. Uses precision etc. from the context (second argument).Context::Type square(const Context::Type &, const Context &): squares the first operand and returns the result. Uses precision etc. from the context (second argument).
Three-operand forms
Besides the above operators, context types are also expected to have three-operand forms for most of these operators (for binary operations, and two-operand forms for unary operators). For all types, the following three-operand forms are expected:
void add(Context::Type &, const Context::Type &, const Context::Type &): adds the second and third operand and stores the result in the first.void addmul(Context::Type &, const Context::Type &, const Context::Type &)multiplies the second and third operand and adds the result to the first operand.void sub(Context::Type &, const Context::Type &, const Context::Type &): subtracts the third from the second operand and stores the result in the first.void submul(Context::Type &, const Context::Type &, const Context::Type &)multiplies the second and third operand and subtracts the result from the first operand.void mul(Context::Type &, const Context::Type &, const Context::Type &): multiplies the second with the third operand and stores the result in the first.void div(Context::Type &, const Context::Type &, const Context::Type &): divides the second by the third operand and stores the quotient in the first.void mod(Context::Type &, const Context::Type &, const Context::Type &): divides the second by the third operand and stores the remainder in the first.void shl(Context::Type &, const Context::Type &, const Context::Type &): multiplies the second operand by 2 to the power of the third operand and stores the result in the first.void shl(Context::Type &, const Context::Type &, long): multiplies the second operand by 2 to the power of the third operand and stores the result in the first.void shl(Context::Type &, const Context::Type &, const arithmetic::Integer &): multiplies the second operand by 2 to the power of the third operand and stores the result in the first.void shr(Context::Type &, const Context::Type &, const Context::Type &): multiplies the second operand by 2 to the power of the third operand and stores the result in the first.void shr(Context::Type &, const Context::Type &, long): multiplies the second operand by 2 to the power of the third operand and stores the result in the first.- Context::Type &, const arithmetic::Integer &)`: multiplies the second operand by 2 to the power of the third operand and stores the result in the first.
The following two-operand forms exist for uniary operators:
void neg(Context::Type &, const Context::Type &): negates the second operand and stores the result in the first.void abs(Context::Type &, const Context::Type &): takes the absolute value of the second operand and stores the result in the first.void square(Context::Type &, const Context::Type &): squares the second operand and stores the result in the first.void increment(Context::Type &, const Context::Type &): increments the second operand by one and stores the result in the first.void decrement(Context::Type &, const Context::Type &): decrements the second operand by one and stores the result in the first.
The following is an abbrevation:
void makeAbs(Context::Type &): makes the operand non-negative by flipping its sign if necessary.
For comparisons, there should exist the following functions:
int compare(const Context::Type &, const Context::Type &): compares the first to the second operand. Returns a negative number if the first is smaller, a positive number if the first is larger, and zero if they are equal.int compareAbsValues(const Context::Type &, const Context::Type &): compares the absolute value of the first to the absolute value of the second operand. Returns a negative number if the first absolute value is smaller, a positive number if the first absolute value is larger, and zero if the absolute values are equal.
For integer types, the following bitwise three-operand and two-operand forms exist:
void band(Context::Integer &, const Context::Integer &, const Context::Integer &): returns the bitwise and of the second and third operand in the first operand.void bor(Context::Integer &, const Context::Integer &, const Context::Integer &): returns the bitwise or of the second and third operand in the first operand.void bxor(Context::Integer &, const Context::Integer &, const Context::Integer &): returns the bitwise exclusive or of the second and third operand in the first operand.void bneg(Context::Integer &, const Context::Integer &): returns the bitwise negation of the second operand in the first operand.
Predicates
For all types, the following predicates exist:
bool isZero(const Context::Type &): returnstrueif and only if the argument is zero.bool isOne(const Context::Type &): returnstrueif and only if the argument is one.bool isPositive(const Context::Type &): returnstrueif and only if the argument is positive.bool isNegative(const Context::Type &): returnstrueif and only if the argument is negative.bool isNonPositive(const Context::Type &): returnstrueif and only if the argument is negative or zero.bool isNonNegative(const Context::Type &): returnstrueif and only if the argument is positive or zero.int sign(const Context::Type &): returns a negative number if the argument is negative, a positive number if it is positive, and zero if it is zero.
For integer types, the following additional predicates exist:
bool isPMOne(const Context::Integer &): returnstrueif and only if the argument is one or minus one.bool isPMTwo(const Context::Integer &): returnstrueif and only if the argument is one or minus two.
Integer Functions
The following functions exists only for integer types:
- Bit access
int bit(const Context::Integer &, long n): returns the value of then-th bit of the absolute value first argument.void setbit(const Context::Integer &, long n, bool value = true): sets the value of then-th bit of the first argument tovalue.long bitLength(const Context::Integer & x): returnsnsuch that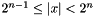 .
.
- Approximated Base-2 Logarithm
long approxLog2(const Context::Integer & x): returns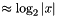 .
.long ceilOfLog2(const Context::Integer & x): returns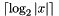 .
.long floorOfLog2(const Context::Integer & x): returns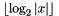 .
.
- Rounded division
void floorDiv(Context::Integer &, const Context::Integer & a, const Context::Integer & b): Computes and stores the result in the first operand.
and stores the result in the first operand.Context::Integer floorDiv(const Context::Integer & a, const Context::Integer & b): Computes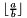 and returns the result.
and returns the result.void ceilDiv(Context::Integer &, const Context::Integer & a, const Context::Integer & b): Computes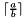 and stores the result in the first operand.
and stores the result in the first operand.Context::Integer ceilDiv(const Context::Integer & a, const Context::Integer & b): Computes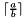 and returns the result.
and returns the result.void roundDiv(Context::Integer &, const Context::Integer & a, const Context::Integer & b): Computes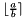 (rounding to the next integer) and stores the result in the first operand.
(rounding to the next integer) and stores the result in the first operand.Context::Integer roundDiv(const Context::Integer & a, const Context::Integer & b): Computes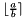 (rounding to the next integer) and returns the result.
(rounding to the next integer) and returns the result.
- Euclidean division
void euclideanDivision(Context::Integer & q, Context::Integer & r, const Context::Integer & a, const Context::Integer & b): Computes an Euclidean Division ofabyb, i.e. computesqandrsuch thata == q * b + rand that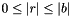 and
and 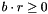 .
.void euclideanDivisionPos(Context::Integer & q, Context::Integer & r, const Context::Integer & a, const Context::Integer & b): Computes an Euclidean Division ofabyb, i.e. computesqandrsuch thata == q * b + rand that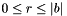 .
.
- Greatest Common Divisors and Least Common Multiples
void GCD(Context::Integer &, const Context::Integer & x, const Context::Integer & y): Computes the non-negative Greatest Common Divisior ofxandyand stores it in the first argument.Context::Integer GCD(const Context::Integer & x, const Context::Integer & y): Computes the non-negative Greatest Common Divisior ofxandyand returns it.void XGCD(Context::Integer & r, Context::Integer & a, Context::Integer & b, const Context::Integer & x, const Context::Integer & y): Computes the non-negative extended Greatest Common Divisiorrofxandy, i.e. computes alsoaandbsuch thatr == x a + b * y.void LCM(Context::Integer &, const Context::Integer & x, const Context::Integer & y): Computes the non-negative Least Common Multiplerofxandyand stores it in the first operand.Context::Integer LCM(const Context::Integer & x, const Context::Integer & y): Computes the non-negative Least Common Multiple ofxandyand returns it.
Uniform Random Number Generator
If the has_uniform_rng property of a context type Context is true, then Context::UniformRNG describes a lightweight object which takes as input a plll::arithmetic::RandomNumberGenerator object (see below), and which provides basic uniform random number generation. The following interface is always provided:
UniformRNG(RandomNumberGenerator &): creates a newContext::UniformRNGobject based on the given random number generator instance.
For integer types, Context::UniformRNG provides the following interface:
void random(Context::Integer & result, const Context::Integer & bound): creates a random number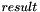 satisfying
satisfying 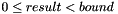 .
.Context::Integer random(const Context::Integer & bound, const Context &): creates and returns a random number satisfying
satisfying 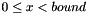 .
.void randomBits(Context::Integer & result, unsigned long bits): createsbitsrandom bits intoresult. That is, it generates a random integer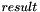 satisfying
satisfying 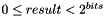 .
.Context::Integer randomBits(unsigned long bits, const Context &): creates and returnsbitsrandom bits. That is, it generates a random integer satisfying
satisfying 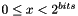 .
.void randomLen(Context::Integer & result, unsigned long bits): creates a random integer inresultof preciselybitsbits. That is, it generates a random integer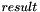 satisfying
satisfying 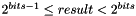 .
.Context::Integer randomLen(unsigned long bits, const Context &): creates a random integer of preciselybitsbits. That is, it generates a random integer satisfying
satisfying 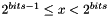 .
.
For real types, on the other hand, the following interface is provided:
void randomUniform(Context::Real &): creates a uniform random number in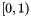 .
.Context::Real randomUniform(const Context &): creates a uniform random number in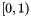 using the given context.
using the given context.
Square Roots and Full Powers
Certain real types provide support for square roots and arbitrary powers. In case of square roots, this is indicated by the has_squareroot property of the context. If it is true, the following functions will be provided:
void sqrt(Context::Real &, const Context::Real &): computes the square root of the second argument and stores it in the first argument.Context::Real sqrt(const Context::Real &): computes and returns the square root of the argument. Note that the return type can be different when expression templates are employed; the return type must be implicitly castable to the typeContext::Real.Context::Real sqrt(const Context::Real &, const Context &): computes and returns the square root of the argument with the precision given by the context. Note that the return type can be different when expression templates are employed; the return type must be implicitly castable to the typeContext::Real.
In any case, the following functions are provided to compute powers – both for real types and integer types:
void square(Context::Type &, const Context::Type &): squares the second argument, and returns the result in the first argument.Context::Type square(const Context::Type &): squares the first argument, and returns the result.void power(Context::Type &, const Context::Type &, long): raises the second argument to the third argument's power, and returns the result in the first argument.Context::Type power(const Context::Type &, long): raises the first argument to the second argument's power, and returns the result.void power(Context::Type &, const Context::Type &, const plll::arithmetic::Integer &): raises the second argument to the third argument's power, and returns the result in the first argument.Context::Type power(const Context::Type &, const plll::arithmetic::Integer &): raises the first argument to the second argument's power, and returns the result.Context::Type operator << (const Context::Type &, long): multiplies the first argument by 2 to the power of the second argument, and returns the result.Context::Type operator >> (const Context::Type &, long): divides the first argument by 2 to the power of the second argument, and returns the result. In the case of integers, rounds towards zero.Context::Type & operator <<= (Context::Type &, long): multiplies the first argument by 2 to the power of the second argument, and stores the result in the first argument.Context::Type & operator >>= (Context::Type &, long): divides the first argument by 2 to the power of the second argument, and stores the result in the first argument. In the case of integers, rounds towards zero.void shl(Context::Type &, const Context::Type &, long): multiplies the second argument by 2 to the power of the third argument and stores the result in the first argument.void shr(Context::Type &, const Context::Type &, long): divides the second argument by 2 to the power of the third argument and stores the result (rounded towards zero) in the first argument.
For real types, the functions returning a Context::Real also accept a const Context & as the third parameter whose precision is used for the result.
For integer types, the following functions are always provided:
void power(Context::Integer &, const Context::Integer &, const Context::Integer &): raises the second argument to the third argument's power, and returns the result in the first argument.Context::Integer power(const Context::Integer &, const Context::Integer &): raises the first argument to the second argument's power, and returns the result.`
For real types, the following functions are only provided if Context::has_full_power is set to true:
void power(Context::Real &, const Context::Real &, const Context::Real &): raises the second argument to the third argument's power, and returns the result in the first argument.Context::Real power(const Context::Real &, const Context::Real &): raises the first argument to the second argument's power, and returns the result.`Context::Real power(const Context::Real &, const Context::Real &, const Context &): raises the first argument to the second argument's power with the precision given by the context, and returns the result.`Context::Real operator << (const Context::Real &, const Context::Real): multiplies the first argument by 2 to the power of the second argument, and returns the result.Context::Real operator >> (const Context::Real &, const Context::Real): divides the first argument by 2 to the power of the second argument, and returns the result.Context::Real & operator <<= (Context::Real &, const Context::Real): multiplies the first argument by 2 to the power of the second argument, and stores the result in the first argument.Context::Real & operator >>= (Context::Real &, const Context::Real): divides the first argument by 2 to the power of the second argument, and stores the result in the first argument.void shl(Context::Real &, const Context::Real &, unsigned const Context::Real): multiplies the second argument by 2 to the power of the third argument and stores the result in the first argument.void shr(Context::Real &, const Context::Real &, unsigned const Context::Real): divides the second argument by 2 to the power of the third argument and stores the result in the first argument.
Trigonometric Functions
If a real type's context Context has Context::has_trigonometric == true, the following trigonometric functions are provided for that type:
- Sine:
void sin(Context::Real &, const Context::Real &): computes the sine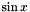 of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real sin(const Context::Real &): computes the sine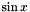 of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real sin(const Context::Real &, const Context &): computes the sine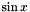 of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.
- Cosine:
void cos(Context::Real &, const Context::Real &): computes the cosine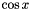 of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real cos(const Context::Real &): computes the cosine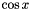 of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real cos(const Context::Real &, const Context &): computes the cosine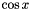 of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.
- Tangent:
void tan(Context::Real &, const Context::Real &): computes the tangent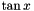 of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real tan(const Context::Real &): computes the tangent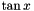 of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real tan(const Context::Real &, const Context &): computes the tangent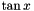 of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.
In case these functions are provided, also the following inverse trigonometric functions are provided for that type:
- Arcsine:
void asin(Context::Real &, const Context::Real &): computes the arcsine![$\arcsin x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_75.png) of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real asin(const Context::Real &): computes the arcsine![$\arcsin x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_75.png) of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real asin(const Context::Real &, const Context &): computes the arcsine![$\arcsin x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_75.png) of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.
- Arccosine:
void acos(Context::Real &, const Context::Real &): computes the arccosine![$\arccos x \in [0, \pi]$](form_76.png) of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real acos(const Context::Real &): computes the arccosine![$\arccos x \in [0, \pi]$](form_76.png) of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real acos(const Context::Real &, const Context &): computes the arccosine![$\arccos x \in [0, \pi]$](form_76.png) of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.
- Arctangent:
void atan(Context::Real &, const Context::Real &): computes the arctangent![$\arctan x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_77.png) of the second argument
of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real atan(const Context::Real &): computes the arctangent![$\arctan x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_77.png) of the first argument
of the first argument  and returns the result.
and returns the result.Context::Real atan(const Context::Real &, const Context &): computes the arctangent![$\arctan x \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$](form_77.png) of the first argument
of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.void atan2(Context::Real &, const Context::Real & y, const Context::Real & x): computes the arctangent![$\arctan \frac{y}{x} \in [-\pi, \pi]$](form_78.png) of the second argument
of the second argument 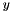 and the third argument
and the third argument  and stores the result in the first argument. The signs of
and stores the result in the first argument. The signs of  and
and 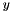 are used to determine the quadrant of the result.
are used to determine the quadrant of the result.Context::Real atan2(const Context::Real & y, const Context::Real & x): computes the arctangent![$\arctan \frac{y}{x} \in [-\pi, \pi]$](form_78.png) of the first argument
of the first argument 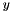 and the second argument
and the second argument  and returns the result. The signs of
and returns the result. The signs of  and
and 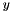 are used to determine the quadrant of the result.
are used to determine the quadrant of the result.Context::Real atan2(const Context::Real & y, const Context::Real & x, const Context &): computes the arctangent![$\arctan \frac{y}{x} \in [-\pi, \pi]$](form_78.png) of the first argument
of the first argument 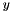 and the second argument
and the second argument  with the precision given by the context and returns the result. The signs of
with the precision given by the context and returns the result. The signs of  and
and 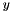 are used to determine the quadrant of the result.
are used to determine the quadrant of the result.
Special Functions
If a real type's context Context has Context::has_special_fns == true, the following special functions are provided for that type:
- Exponential function:
void exp(Context::Real &, const Context::Real &): computes the exponential function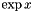 of the second argument
of the second argument  and stores the result in the first argument. Note that
and stores the result in the first argument. Note that 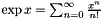 .
.Context::Real exp(const Context::Real &): computes the exponential function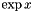 of the first argument
of the first argument  and returns the result. Note that
and returns the result. Note that 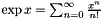 .
.Context::Real exp(const Context::Real &, const Context &): computes the exponential function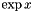 of the first argument
of the first argument  with the precision given by the context and returns the result. Note that
with the precision given by the context and returns the result. Note that 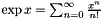 .
.
- Natural logarithm:
void log(Context::Real &, const Context::Real &): computes the natural logarithm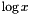 of the second argument
of the second argument  and stores the result in the first argument. Note that
and stores the result in the first argument. Note that 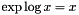 for all
for all 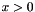 .
.Context::Real log(const Context::Real &): computes the natural logarithm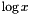 of the first argument
of the first argument  and returns the result. Note that
and returns the result. Note that 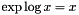 for all
for all 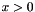 .
.Context::Real log(const Context::Real &, const Context &): computes the natural logarithm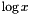 of the first argument
of the first argument  with the precision given by the context and returns the result. Note that
with the precision given by the context and returns the result. Note that 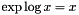 for all
for all 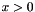 .
.
- Gamma function:
void gamma(Context::Real &, const Context::Real &): computes the Gamma function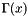 of the second argument
of the second argument  and stores the result in the first argument. Note that
and stores the result in the first argument. Note that 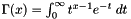 for
for 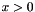 , and that
, and that 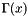 has poles at 0 and the negative integers.
has poles at 0 and the negative integers.Context::Real gamma(const Context::Real &): computes the Gamma function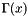 of the first argument
of the first argument  and returns the result. Note that
and returns the result. Note that 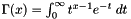 for
for 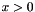 , and that
, and that 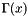 has poles at 0 and the negative integers.
has poles at 0 and the negative integers.Context::Real gamma(const Context::Real &, const Context &): computes the Gamma function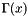 of the first argument
of the first argument  with the precision given by the context and returns the result. Note that
with the precision given by the context and returns the result. Note that 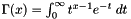 for
for 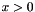 , and that
, and that 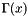 has poles at 0 and the negative integers.
has poles at 0 and the negative integers.
- Natural logarithm of the absolute value of the Gamma function:
void lgamma(Context::Real &, const Context::Real &): computes the logarithm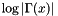 of the absolute value of the Gamma function of the second argument
of the absolute value of the Gamma function of the second argument  and stores the result in the first argument.
and stores the result in the first argument.Context::Real lgamma(const Context::Real &): computes the logarithm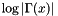 of the absolute value of the Gamma function of the first argument
of the absolute value of the Gamma function of the first argument  and returns the result.
and returns the result.Context::Real lgamma(const Context::Real &, const Context &): computes the logarithm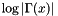 of the absolute value of the Gamma function of the first argument
of the absolute value of the Gamma function of the first argument  with the precision given by the context and returns the result.
with the precision given by the context and returns the result.void lgamma(Context::Real &, int &, const Context::Real &): computes the logarithm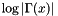 of the absolute value of the Gamma function of the third argument
of the absolute value of the Gamma function of the third argument  and stores the result in the first argument. The sign of
and stores the result in the first argument. The sign of  is stored in the second variable by 1 for
is stored in the second variable by 1 for 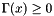 and -1 for
and -1 for 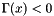 .
.Context::Real lgamma(int &, const Context::Real &): computes the logarithm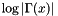 of the absolute value of the Gamma function of the second argument
of the absolute value of the Gamma function of the second argument  and returns the result. The sign of
and returns the result. The sign of 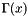 is stored in the second variable by 1 for
is stored in the second variable by 1 for 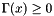 and -1 for
and -1 for 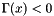 .
.Context::Real lgamma(int &, const Context::Real &, const Context &): computes the logarithm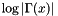 of the absolute value of the Gamma function of the second argument
of the absolute value of the Gamma function of the second argument  with the precision given by the context and returns the result. The sign of
with the precision given by the context and returns the result. The sign of 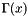 is stored in the second variable by 1 for
is stored in the second variable by 1 for 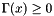 and -1 for
and -1 for 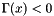 .
.
Constants
If a real type's context Context has Context::has_constants == true, the following constants are provided for that type:
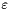 : the smallest positive number such that
: the smallest positive number such that 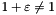 (this only makes sense for approximate floating point types). This is also called the machine precision constant.
(this only makes sense for approximate floating point types). This is also called the machine precision constant.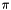 : the circle number, such that a circle of radius
: the circle number, such that a circle of radius 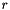 has area
has area 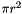 and circumference
and circumference 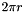 .
.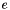 : the Euler number
: the Euler number 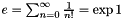 .
.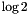 : the natural logarithm of 2.
: the natural logarithm of 2.
These variables can be accessed by the following member functions of a real Context:
Context::Real getEpsilon() const: returns the machine precision constant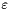 .
.void getEpsilon(Context::Real &) const: stores the machine precision constant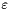 in the argument.
in the argument.Context::Real getPi() const: returns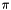 .
.void getPi(Context::Real &) const: stores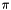 in the argument.
in the argument.Context::Real getEuler() const: returns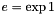 .
.void getEuler(Context::Real &) const: stores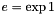 in the argument.
in the argument.Context::Real getLog2() const: returns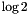 .
.void getLog2(Context::Real &) const: stores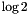 in the argument.
in the argument.
Traits
If T is a type, then plll::arithmetic::traits::type_traits<T> retrieves some basic information and arithmetic properties of T. The traits are mainly used by the conversion functions (see Conversions), but can also be used independently of these.
Traits are only defined for native types such as signed int, unsigned long and double, for string types such as const char * and std::string, and for arithmetic types given by contexts as above.
The following properties are defined in all defined type_traits<> instances:
is_number:truefor arithmetic (number) types.is_realtype:truefor arithmetic types which are real types (such as floating point types or rational numbers). Alwaysfalseifis_numberisfalse.is_inttype:truefor arithmetic types which are integer types. Alwaysfalseifis_numberisfalse.is_string:truefor string types. Alwaysfalseifis_numberistrue.
- Todo:
- Implement support for other character types than
char(likewchar_t, and also new C++11 strings)
is_cpp_string:trueforstd::string. Alwaysfalseifis_stringisfalse.is_c_string:trueforchar *andconst char *. Alwaysfalseifis_stringisfalse.
For number types, i.e. if is_number is true, the following properties are defined:
is_cputype:truefor native types supported by CPU (or emulated natively on CPUs, such aslong doubleon most UltraSPARC CPUs).is_exact:truefor types which do use approximations (like floating point types). For example, for GMP and CPU integers, this is alwaystrue.has_infinity:truefor types having objects representing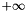 and
and 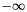 .
.has_uniform_rng:trueif the type provides a uniform random number generator. Such a context exhibits a typeUniformRNG, whose interface will be described in more detail above in Uniform Random Number Generator. Note that the rational number context fromrational.hppis an example of a context not providing a uniform random number generator.has_context:trueif this type has an associated context as described in Contexts. Ifhas_contextistrue, a typedefContextyields the context type.is_native:trueonly for native typesint,long,long long,float,double,long doubleand the unsigned counterparts of the integer types.
For number types, also the following types are defined:
PromoteType: another type to which automatic promotes are a good idea. For example,intandunsigned inthavePromoteTypedefined aslongandunsigned long, respectively. For most types,PromoteTypeequalsT. There must always be implicit conversions fromTtoPromoteType, which are required to be very efficient.ConstReferenceType: the preferred way of passing an equivalent of a const reference. This is often equal toconst T &, but might also beTfor native types and encapsulated native types for which a reference yields unnecessary overhead (because copying is very cheap).
For integer types, the following property is available in addition to the above general properties:
is_modulo:truefor types which are "wrap around", such as native integer arithmetic which in fact computes in rings such as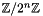 .
.
For integer types, all other properties defined for real types – is_variable_precision, has_squareroot, has_full_power, has_special_fns, has_huge_exponents, has_constants, has_trigonometric – are set to false. Vice versa, for real types, is_modulo is set to false.
For real types, is_modulo is always false. Real types have the following properties:
is_variable_precision:trueif the precision of the type can be modified.has_squareroot:trueif (approximated) square roots are supported. This will befalsefor rational numbers, buttruefor most (or even all) floating point types. For more information, see Square Roots and Full Powers.has_full_power:trueif elements can be raised to fractional powers (where the powers are coming from the same context). This will befalsefor rational numbers, buttruefor most (or even all) floating point types. For more information, see Square Roots and Full Powers.has_special_fns:trueif special functions such aslgammaetc. are supported for this type. A list of special functions with explanations can be found above in Special Functions.has_huge_exponent:truefor floating point types using at least the range of asigned intfor the exponent. If the exponent range is (much) smaller, this has to be set tofalse.has_constants:trueif special constants such as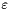 ,
, 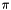 ,
, 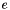 and
and 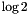 are provided by the context. See above in Constants for more information.
are provided by the context. See above in Constants for more information.has_trigonometric:trueif trigonometric functions such assinandcosare provided. See above in Trigonometric Functions for more information.
Conversions
Conversions with Contexts
Assume we are given a context Context with instantiation c, a variable v of type Context::Type, and another variable w of another type. To store into v the converted value of w, we can use one of the two following calls:
convert(v, w, c),c = convert(w, c).
If w2 is another variable of the same type as w, and if Context::is_realtype is true, we can also convert the fraction w/w2 by calling:
convert_fraction(v, w, w2, c),v = convert_fraction(w, w2, c).
In case w is a real type and v is an integer type (i.e. Context::is_inttype is true), the following calls allow to convert the floor of w, the ceiling of w or a rounded value of w to v:
convert_floor(v, w, c),v = convert_floor(w, c),convert_ceil(v, w, c),v = convert_ceil(w, c),convert_round(v, w, c),v = convert_round(w, c).
In case we want to know whether w was rounded up or down to achieve v in the last two calls, we can use the following syntax:
convert_round(v, w, rounded_up, c),v = convert_round(w, rounded_up, c);
here, rounded_up must be a non-const variable of type bool, which is set to true in case w was rounded up, and set to false in case w was rounded down. Note that this is not always accurate, as the rounding is often done before the conversion and the conversion might modify the value due to precision restrictions of the destination type.
Conversions to Native Types
Note that while the above functions also work with native types for w and w2, they cannot be used to convert to a native type (since they don't have contexts). To convert w to, say, an int, we have to use special forms:
v = convert<T>(w),v = convert_floor<T>(w),v = convert_ceil<T>(w),v = convert_round<T>(w),v = convert_round<T>(w, rounded_up).
Here, T can be any of int, long, long long, float, double, long double and their unsigned counterparts.
As a special case, T can also be plll::arithmetic::Integer, which allows to create arbitrary precision integers using the same syntax.
Conversions to and from Strings
To (try to) convert a string to a type, with or without context, one can also use the above conversion functions. If s is a string, i.e. of types char *, const char * or std::string, it can be converted to a variable v of type Context::Type by
convert(v, s, c),v = convert(s, c),
or to a variable n of native type T (or plll::arithmetic::Integer) by
n = convert<T>(s).
To convert a variable to a string, note that only conversion to std::string is allowed to avoid the many pitfalls with C strings (char * and const char *). For this, also the native conversion can be used:
s = convert<std::string>(v);
here, v can be a type with context, or a native type without context.
Another way to convert numbers to strings is to use the arithmetic::StringContext and its derived types, arithmetic::HexStringContext and arithmetic::OctalStringContext. With them, one can use the usual convert() function: if v is a number and s a std::string variable,
s = convert(v, s, arithmetic::StringContext()),s = convert(v, arithmetic::StringContext()).
Instead of using the default constructor arithmetic::StringContext::StringContext(), which generates a arithmetic::StringContext object for base 10 (decimal) conversion, one can also specify a base via the arithmetic::StringContext::StringContext(unsigned) context, or use arithmetic::HexStringContext to fix base 16 (hexadecimal) or arithmetic::OctalStringContext to fix base 8 (octal).
Note that types do not have to support all bases. Floating point types might support only base 10, and integer types might only support bases 8, 10 and 16. Only plll::arithmetic::Integer is guaranteed to support bases 2 to 36.
Result Types of Arithmetic Operations
In C++11, it is simple to find out the result of a operation such as a + b using decltype(). Unfortunately, in C++03 and C++98, this is not available. Additionally, when using expression templates, a finer distinction between intermediate result of a + b, which might be something like addition<Type, Type>(a, b), and the finaly type of a + b, which will be something like Type, can be quite important.
The utility templates plll::arithmetic::binary_operation<> and plll::arithmetic::unary_operation<> provide such information. Each instance provides some properties as well as two types: ResultType, the final result type, and IntermetiateType, the intermediate result type.
The two properties are:
supported:trueif information about these types is available. Usuallyfalsenever appears since in that case, the template is usually not defined.intermediate_expression:trueif an intermediate expression is returned which is not of the final type. More precisely,trueif and only ifResultTypeis not equal toIntermediateType.
To query the result of a binary expression such as a + b, one has to use the plll::arithmetic::binary_operation template:
plll::arithmetic::binary_operation<Type_of_A, Type_of_B, operation>
Here, operation is one of the classes plll::arithmetic::op::addition for addition, plll::arithmetic::op::subtraction for subtraction, plll::arithmetic::op::multiplication for multiplication, plll::arithmetic::op::division for division, and plll::arithmetic::op::modulo for modulo.
To query the result of a unary expression such as -a, one has to use the plll::arithmetic::unary_operation template:
plll::arithmetic::unary_operation<Type_of_A, operation>
Here, operation must be plll::arithmetic::op::negation for negation.
A possible use-case is a proxy function which should return the product of two elements, like coefficients of a vector or a matrix. We know that the coefficients have types A and B. Then the return type of the function should better be plll::arithmetic::binary_operation<A, B, plll::arithmetic::op::multiplication>::IntermediateType to avoid too early evaluation. Extensive examples can be found in the matrix and vector classes; see Matrices and Vectors.
Available Contexts
Main Arithmetic
The following contexts are always made available in the plll library:
plll::arithmetic::IntegerContext: a context providing arbitrary-precision integer arithmetic;plll::arithmetic::RealContext: a context providing arbitrary-precision floating point arithmetic;plll::arithmetic::RationalContext(inrational.hpp): a context providing arbitrary-precision rational arithmetic;plll::arithmetic::NIntContext<T>(inarithmetic-nint.hpp): an integer context for the native CPU integer typesT == int,T == longandT == long long.
Note that the corresponding types for the first three contexts, plll::arithmetic::Integer, plll::arithmetic::Real and plll::arithmetic::Rational, all employ expression templates to increase efficiency. Therefore, writing
v = a * b;
instead of
mul(v, a, b);
will make no difference. In fact, both lines should compile to exactly the same result. This is also the case for add-mul and sub-mul statements such as
v += a * b v -= a * b
which should compile to
addmul(v, a, b); submul(v, a, b);
For plll::arithmetic::Integer and plll::arithmetic::Real, these instructions have implementations tailored to this situation which will often appear during vector and matrix operations, such as computing dot products, squared norms and matrix-matrix and matrix-vector products.
Internal Floating Point Arithmetic
Besides the above basic contexts, more contexts are used internally which are (currently) not exposed to the end user:
plll::arithmetic::NFPContext<T>: a real context for the native floating point typesT == float,T == doubleandT == long double;plll::arithmetic::DDQDContext<T>: a real context for the double double and quad double typesdd_realandqd_realfrom theqdquad double library.
Note that the double double and quad double types are not available on every platform. Currently, to use these contexts outside the library, one has to include the corresponding files from the plll/include-internal path inside the plll distribution.
Combining with GMP and MPFR
Since plll::arithmetic::Integer is based on GMP's mpz_t and plll::arithmetic::Real is based on MPFR's mpfr_t, it is possible to manipulate such objects directly with GMP or MPFR functions, or transfer data between plll::arithmetic::Integer and plll::arithmetic::Real objects and their GMP and MPFR counterparts. To make this possible, both plll::arithmetic::Integer and plll::arithmetic::Real provide methods getInternal(), which provide a reference to the underlying mpz_t (for integers) respectively mpfr_t (for floating point numbers) object.
Use these functions with care, as most of plll is agnostic to the underlying library used for arbitrary-precision integers and floating point numbers, and thus the underlying libraries (now GMP and MPFR) might be exchanged with other libraries at some time.
Also note that plll changes the memory allocators for both GMP and MPFR when calling initArithmeticThreadAllocators(). This should be done once at the very beginning of the program, before any plll::arithmetic::Integer or plll::arithmetic::Real object is created, and once at the start of every new thread. This will enable thread-local allocators for GMP and MPFR objects, which increases the performance of plll in multithreaded environments dramatically, especially if many threads are used concurrently (for example, during parallel enumeration).
