How lattice reduction works

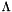If we are given a basis $b_1, \dots, b_k$ of a lattice $\Lambda$ , we have

$\det \Lambda \le \prod_{i=1}^k \|b_i\|,$

with equality if and only if the 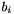$b_i$ 's are pairwise orthogonal. (Here, 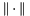$\|\cdot\|$ denotes the Euclidean norm on 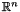$\mathbb{R}^n$ .) The less orthogonal the vectors are, the larger the product on the right-hand side is. One notion of lattice reduction is to minimize the difference between the product on the right-hand side and the determinant 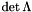$\det \Lambda$ : then the vectors 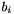$b_i$ must be relatively short.

This motivates the idea of size reduction: for this, one first computes the Gram-Schmidt orthogonalization of $b_1, \dots, b_k$ by iteratively, 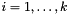$i = 1, \dots, k$ , computing:

$\mu_{ij} := \frac{\langle \hat{b}_i, \hat{b}_j \rangle}{\langle \hat{b}_i, \hat{b}_i \rangle} \quad \text{for } j = 1, \dots, i - 1, \quad \text{and} \quad \hat{b}_i := b_i - \sum_{j=1}^{i-1} \mu_{ij} \hat{b}_j.$

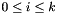The resulting vectors $\hat{b}_1, \dots, \hat{b}_k$ are pairwise orthogonal and the subvector space spanned by $b_1, \dots, b_i$ is also generated by $\hat{b}_1, \dots, \hat{b}_i$ , $0 \le i \le k$ .

Essentially, 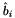$\hat{b}_i$ is the orthogonal projection of 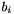$b_i$ onto the orthogonal complement of the span of 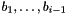$b_1, \dots, b_{i-1}$ . Denote this projection by 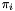$\pi_i$ ; then 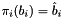$\pi_i(b_i) = \hat{b}_i$ , and more generally

$\pi_j(b_i) = \sum_{\ell=j+1}^i \mu_{i\ell} \hat{b}_\ell, \qquad 0 \le j \le i.$

Since the 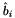$\hat{b}_i$ 's are pairwise orthogonal, we get

$\|\pi_j(b_i)\|^2 = \sum_{\ell=j+1}^i \mu_{i\ell}^2 \|\hat{b}_\ell\|^2.$

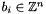While the vectors $\hat{b}_1, \dots, \hat{b}_k$ are pairwise orthogonal and generate the same subvector space as $b_1, \dots, b_k$ , they do in general not generate the same lattice. In fact, even if $b_i \in \mathbb{Z}^n$ for every 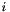$i$ , it could be that 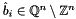$\hat{b}_i \in \mathbb{Q}^n \setminus \mathbb{Z}^n$ for every $i > 1$ .

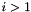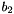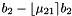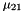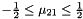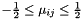To obtain a basis of the same lattice which is somewhat more orthogonal than the original basis, one can replace $b_2$ by $b_2 - \lfloor \mu_{21} \rceil b_2$ ; if one computes $\mu_{21}$ of the resulting new basis, one obtains $-\tfrac{1}{2} \le \mu_{21} \le \tfrac{1}{2}$ . 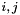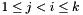Iteratively repeating this, one obtains a basis $\tilde{b}_1, \dots, \tilde{b}_k$ of the same lattice which satisfies $-\tfrac{1}{2} \le \mu_{ij} \le \tfrac{1}{2}$ for every $i, j $ with $1 \le j < i \le k$ . Such a basis is called size reduced, and the process of reaching such a basis is called size reduction.

Essentially all lattice reduction algorithms can be described by alternating the process of size reduction with another operation.

Basic reduction: LLL and friends

For a basis to be LLL-reduced (with reduction parameter $\alpha \in (1/4, 1]$ ), one requires it to be size reduced and satisfy the Lovász condition:

$\alpha \cdot \|\pi_i(b_i)\|^2 \le \|\pi_i(b_{i+1})\|^2 \quad \text{for all } i = 1, \dots, k - 1.$

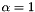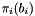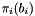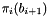For $\alpha = 1$ , this condition ensures that $\pi_i(b_i)$ is a shortest vector in the lattice spanned by $\pi_i(b_i)$ and $\pi_i(b_{i+1})$ .

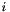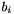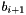The LLL reduction algorithm is performed by finding the smallest $i$ for a sized reduced basis $b_1, \dots, b_k$ for which this inequality is not satisfied, and switching $b_i$ and $b_{i+1}$ and repeating by first size reducing and then finding the then minimal 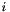$i$ . If no such 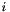$i$ is found, the algorithm is done. In case 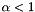$\alpha < 1$ , A. Lenstra, H. Lenstra and L. 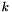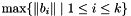Lovász [9] showed that the algorithm terminates in time polynomially in $k$ and $\max\{ \|b_i\| \mid 1 \le i \le k \}$ (assuming 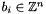$b_i \in \mathbb{Z}^n$ for every 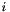$i$ ). For 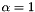$\alpha = 1$ , it is not even known whether the algorithm terminates in general.

Note that a 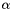$\alpha$ -LLL reduced basis satisfies

$\|b_1\| \le (\alpha - 1/4)^{-(k-1)/2} \cdot \lambda_1(\Lambda) \quad \text{and} \quad \|b_1\| \le (\alpha - 1/4)^{-(n - 1)/4} \cdot (\det \Lambda)^{1/n}.$

Here,

$\lambda_1(\Lambda) := \min\{ \|v\| \mid v \in \Lambda \setminus \{ 0 \} \}$

denotes the length of a shortest non-zero vector of 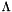$\Lambda$ .

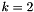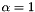Note that if $k = 2$ and $\alpha = 1$ , the algorithm is guaranteed to terminate and yield a shortest vector of the lattice. In that case, the algorithm is equal to an algorithm already known go Gauss, called Gauss reduction.

There exist variations of the LLL algorithm. They usually relax/replace the Lovász condition, such as by the Siegel condition

$\tfrac{3}{4} \cdot \alpha \cdot \|\pi_k(b_k)\|^2 > \|\pi_{k+1}(b_{k+1})\|^2,$

, or by adding additional constraints, such as in the case of Deep Insertions [15].

Strong reduction: SVP and HKZ bases

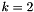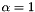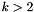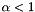While for $k = 2$ and $\alpha = 1$ , LLL reduction produces a shortest vector, this is not necessarily true as soon as $k > 2$ or $\alpha < 1$ . In fact, Schnorr showed that the bound 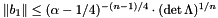$\|b_1\| \le (\alpha - 1/4)^{-(n - 1)/4} \cdot (\det \Lambda)^{1/n}$ is sharp.

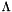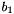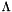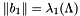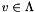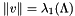Nonetheless, a shortest vector exists for the lattice. We call a basis $b_1, \dots, b_k$ of $\Lambda$ a SVP basis if $b_1$ is a shortest vector of $\Lambda$ ; in other words, it is a SVP basis iff $\|b_1\| = \lambda_1(\Lambda)$ . Here, SVP stands for *Shorest Vector Problem", which denotes the problem of finding a vector $v \in \Lambda$ with $\|v\| = \lambda_1(\Lambda)$ .

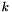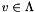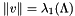A SVP basis can be computed practically, but the fastest algorithms are of single exponential complexity in $k$ ; in fact, it was proven by Ajtai that computing $v \in \Lambda$ with $\|v\| = \lambda_1(\Lambda)$ is NP hard (under randomized reductions) [1]. Assuming that there are no subexponential or even polynomial algorithms to solve NP hard problems, such algorithms are essentially optimal from an asymptotic point of view.

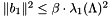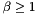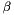In case $\|b_1\|^2 \le \beta \cdot \lambda_1(\Lambda)^2$ for some $\beta \ge 1$ , $b_1, \dots, b_k$ is called a * $\beta$ -SVP basis*. Most of the time, such bases are computed by computing a shortest vector, comparing its length to 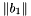$\|b_1\|$ , and replacing 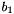$b_1$ by that vector only if it is shorter by a factor of at least 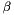$\beta$ . The notion of 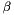$\beta$ -SVP bases is mostly used during other reduction algorithms.

Since ( 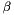$\beta$ -)SVP bases are only defined by a property on their first vector, all other vectors can be quite large and "ugly". Therefore, one is interested in also reducing them. A good notion is the one of a * 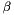$\beta$ -Hermite-Korkine-Zolotarev (HKZ) basis*, where one requires a basis $b_1, \dots, b_k$ to be size reduced and to satisfy

$\|\pi_i(b_i)\|^2 \le \beta \cdot \lambda_1(\Lambda(\pi_i(b_i), \dots, \pi_i(b_k)))^2 \quad \text{for all } i \in \{ 1, \dots, k \}.$

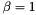Again, if $\beta = 1$ , $b_1, \dots, b_k$ is just called a HKZ basis (instead of 1-HKZ basis). A HKZ basis can be computed by iteratively computing SVP bases and doing size reduction. The required running time is up to a polynomial factor identical to the one for computing a single SVP basis for lattices of rank 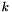$k$ .

Intermediate reduction: BKZ and friends

While the exponential time SVP/HKZ basis reduction algorithms compute a shortest vector for the whole lattice, the polynomial time LLL algorithm only computes shortest vectors for two-dimensional orthogonally projected lattices 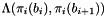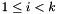$\Lambda(\pi_i(b_i), \pi_i(b_{i+1}))$ , $1 \le i < k$ . Schnorr suggested [16] to interpolate between these two extrema by considering orthogonally projected lattices of larger rank.

Fixing a block size 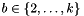$b \in \{ 2, \dots, k \}$ , a basis is * 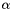$\alpha$ -BKZ reduced* with blocksize 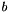$b$ * if it is size-reduced and if

$\alpha \cdot \|\pi_i(b_i)\|^2 \le \lambda_1(\Lambda(\pi_i(b_i), \dots, \pi_i(b_{\min\{ i+b-1, k \}})))^2 \quad \text{for all } i \in \{ 1, \dots, k \}.$

Schnorr and Euchner showed [15] that a 1-BKZ reduced basis with blocksize 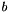$b$ satisfies

$\|b_1\|^2 \le b^{(1+\log b) (k-1)/(b-1)} \cdot \lambda_1(\Lambda)^2$

in case $b-1$ divides $k-1$ .

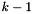BKZ is currently the most practical lattice reduction algorithm to find short vectors in all dimensions. Playing with the block size 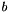$b$ and the reduction parameter 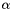$\alpha$ as well as introducing early aborts (i.e. stopping the lattice reduction after a specified time or when a short enough vector is found) allow to adjust the algorithm to many practical situations.

Supported algorithms

In this section, we will discuss the algorithms provided by this library.

LLL-like reduction

plll implements several variants of the LLL algorithm. They differ only by their choice of the swap condition. Deep Insertions are implemented orthogonally to this and can be enabled for LLL- and BKZ-type algorithms; this is described in Deep Insertions.

Classic LLL

The original condition by A. Lenstra, H. Lenstra and L. Lovász [9], called the Lovász condition (see Basic reduction: LLL and friends), which compares the projected lengths of two adjacent vectors, where the vectors are projected onto the orthogonal complement of all previous vectors.

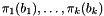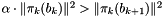In terms of the Gram-Schmidt orthogonalization $\pi_1(b_1), \dots, \pi_k(b_k)$ of the basis $b_1, \dots, b_k$ , this condition can be expressed as $\alpha \cdot \|\pi_k(b_k)\|^2 > \|\pi_k(b_{k+1})\|^2$ .

Classic LLL reduction can be used by calling plll::LatticeReduction::lll() with the LLL mode plll::LatticeReduction::LLL_Classic.

Unprojected LLL

This variant of LLL uses a simpler condition, which compares the unprojected lengths of two adjacent basis vector. This essentially attempts to sort the vectors by increasing (unprojected) length while at the same time size-reducing the basis.

In terms of the basis $b_1, \dots, b_k$ , this condition can be expressed as $\alpha \cdot \|b_k\|^2 > \|b_{k+1}\|^2$ .

Unprojected LLL reduction can be used by calling plll::LatticeReduction::lll() with the LLL mode plll::LatticeReduction::LLL_Unprojected.

Siegel LLL

This variant of LLL uses a simpler condition, which allows to prove the same bounds on the output quality, called the Siegel condition. Note that the Lovász condition implies the Siegel condition.

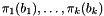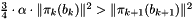In terms of the Gram-Schmidt orthogonalization $\pi_1(b_1), \dots, \pi_k(b_k)$ of the basis $b_1, \dots, b_k$ , this condition can be expressed as $\frac{3}{4} \cdot \alpha \cdot \|\pi_k(b_k)\|^2 > \|\pi_{k+1}(b_{k+1})\|^2$ .

Siegel LLL reduction can be used by calling plll::LatticeReduction::lll() with the LLL mode plll::LatticeReduction::LLL_Siegel.

BKZ-like reduction

The plll library implements many different BKZ variants. They all have in common that they opreate by applying SVP or HKZ basis computations to projected blocks (or their duals).

Schnorr-Euchner BKZ

The classical Schnorr-Euchner BKZ algorithm, as described by C.-P. Schnorr and M. Euchner in Section 6 of [15].

Schnorr-Euchner BKZ reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_SchnorrEuchner.

Simplified BKZ

A simplified version of the BKZ algorithm, as described by G. Hanrot, X. Pujol and D. Stehle in [8].

Simplified BKZ reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_Simplified.

Terminating BKZ

A "Terminating BKZ" variant of the simplified version of the BKZ algorithm, as described by G. Hanrot, X. Pujol and D. Stehle in [8]. There are two versions. The first computes Hermite-Korkine-Zolotarev (HKZ) bases for every block, and the second Shortest Vector (SVP) bases for every block.

Terminating BKZ reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_HanrotPujolStehleHKZ respectively plll::LatticeReduction::BKZ_HanrotPujolStehleSVP.

Primal-Dual BKZ

The primal-dual BKZ algorithm by H. Koy, as described in Section 3 of [17].

This implementation is a mixture of three slightly varying descriptions of the algorithms:

the description by H. Koy in the slides from 2004, available here;
the description by C.-P. Schnorr in Section 3 of [17];
the description by C.-P. Schnorr in the lecture notes "Gitter und Kryptographie".

The basic idea of the algorithm is to first run LLL on the whole basis and then HKZ on the first block is from [17]. That each round starts by HKZ-reducing the block 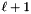$\ell+1$ is shared by [17] and the lecture notes, while in Koy's slides, only an SVP basis is computed.

As the next step, in Koy's slides a DSVP basis is computed for block 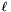$\ell$ , while in the lecture notes a dual HKZ basis is computed, and [17] computes a dual HKZ basis but only applies the transformation conditionally. In the three sources, the aim is to maximize the norm of the last GS vector in the 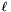$\ell$ -th block.

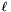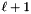In [17] and the lecture notes, a LLL step is applied to both blocks $\ell$ and $\ell+1$ ; in case a swap appeared between the two blocks, the changes are taken. (In [17], the HKZ reduction of the dual of block 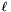$\ell$ is only applied to the basis in this case. In the lecture notes, the HKZ reduction of the dual is always applied.) In Koy's slides, one checks the Lovász condition for the two vectors where the blocks meet, and if it is not satisfied LLL reduction is applied to both blocks.

Finally, in [17], no size reduction is applied. In the lecture notes, size reduction is applied only at the very end of the algorithm (and the algorithm never increases 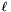$\ell$ ). In Koy's slides, size reduction is not mentioned.

This implementation is close to Koy's slides, with an additional swap for the adjacent vectors before running LLL. Additionally, we run size reduction at the end as in the lecture notes.

Primal-Dual BKZ reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_PrimalDual.

Slide Reduction

The slide reduction algorithm, as described by N. Gama and P. Q. Nguyen in [5].

Slide reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_SlideReduction.

Improved Slide Reduction

A improved and accelerated version of Slide Reduction, as described in [18] by C.-P. Schnorr (Section 3).

Improved slide reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_ImprovedSlideReduction.

Note that in the paper, Schnorr describes two variations:

One variation uses a larger dual SVP enumeration and a single primal SVP enumeration. That one can be used with the BKZ mode plll::LatticeReduction::BKZ_ImprovedSlideReduction2.
The other variation uses a single larger primal SVP enumeration and one dual SVP enumeration. That one can be used with the BKZ mode plll::LatticeReduction::BKZ_ImprovedSlideReduction3.

Semi-Block-2k-Reduction

The semi block 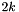$2k$ -reduction, as described in [17] by C.-P. Schnorr (Section 2).

This implementation is a mixture of four varying descriptions of the algorithms:

C.-P. Schnorr: "A Hierarchy of Polynomial Time Lattice Basis Reduction" [16];
C.-P. Schnorr: "Blockwise Lattice Basis Reduction Revisited" [17];
C.-P. Schnorr: "Gitter und Kryptographie"; lecture notes, available here;
C.-P. Schnorr: "Progress on LLL and Lattice Reduction"; Chapter 4 in [13].

In [16], first all blocks are HKZ reduced. Then, one selects the smallest i such that the determinant or the Siegel condition are violated. In the latter case, an LLL step is applied to the two vectors, and both adjacent blocks are HKZ reduced. In the former case, one applies HKZ to the combined block (of double size). This is repeated until the two conditions are always satisfies.

In [17], one first computes a HKZ basis of the first block, then applies LLL to the whole lattice. Then, for each 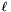$\ell$ , one first HKZ-reduces block 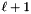$\ell+1$ . Then one tests whether swapping the adjacent vectors from the two blocks shortens the GS norm of the last vector of the 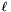$\ell$ -th block by at least a factor of 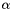$\alpha$ . Finally, the double block is always HKZ reduced, though the changes are not directly applied. (It is not totally clear to me if the double block HKZ reduction is always applied, or only if the swap occured.) Then, the new determinant for block 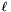$\ell$ (after HKZ-reduction of double block) is computed and compared to the old; if it decreased by a factor of at least 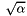$\sqrt{\alpha}$ , the changes from the double block HKZ reduction are applied and 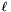$\ell$ is decreased. Otherwise, the double-block HKZ-reduction changes are ignored and 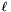$\ell$ is increased.

In the lecture notes, one first computes an LLL basis of the whole lattice, and then a HKZ basis of the first block. Then, for each 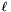$\ell$ , one first HKZ-reduces block 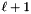$\ell+1$ . Then, one applies HKZ reduction to the double block 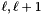$\ell,\ell+1$ , but does not directly apply the changes. As in [17], they are only applied if the determinant of block 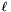$\ell$ decreases by a certain factor (which can be different from the LLL 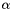$\alpha$ ). At the very end of the algorithm, size reduction is applied to the basis.

In [13], one first computes an LLL basis of the whole lattice, and then a HKZ basis of the first block. Then, for each 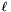$\ell$ (starting with 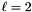$\ell = 2$ ), one first HKZ-reduces block 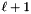$\ell+1$ . Then, one applies LLL reduction to the double block 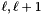$\ell,\ell+1$ , but does not directly apply the changes. If an LLL swap connects the two blocks, the LLL reduction is applied, 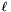$\ell$ decreased, and one restarts with this 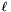$\ell$ . In case no connecting swap appears, one throws away the changes and instead HKZ-reduces the double block 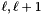$\ell,\ell+1$ . As in [17] and the lecture notes, one only applies the changes from the HKZ reduction in case the determinant decreases by a certain factor; in that case, 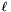$\ell$ is decreased, otherwise increased. In case 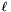$\ell$ is 1, one restarts the whole algorithm (beginning with LLL-reducing the basis); otherwise one continues with the new value of $\ell$ .

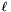Semi block 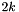$2k$ -reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_SemiBlock2k.

Sampling Reduction

The Sampling Reduction, as described by J. A. Buchmann and C. Ludwig in [2].

Sampling reduction can be used by calling plll::LatticeReduction::bkz() with the BKZ mode plll::LatticeReduction::BKZ_SamplingReduction.

SVP solvers

Up to dimension 30, all SVP problems are solved by enumeration, except if a specific SVP solver is requested (and then only on the highest reduction hierarchy level). The enumeration code there is a simplified version of the Kannan-Schnorr-Euchner enumeration below and does not call any callback function.

The default choice for enumeration is the parallel Kannan-Schnorr-Euchner enumeration if more than one core is available, and the usual Kannan-Schnorr-Euchner enumeration otherwise. In practice, it is recommended to use parallel enumeration only for higher dimensions, say 50 and above.

Kannan-Schnorr-Euchner enumeration

A variant of the Kannan-Schnorr-Euchner enumeration algorithm [15] with various improvements; see, for example, Appendix B of [7] by N. Gama, P. Q. Nguyen and O. Regev.

A parallelized variant of the Kannan-Schnorr-Euchner enumeration algorithm with various improvements. The parallelization uses multiple cores. There is almost no communication between cores, except if a shorter vector is found by one, or if one core runs out of work and asks others to split their workload.

Parallel or non-parallel Kannan-Schnorr-Euchner enumeration can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_ParallelKannanSchnorrEuchner respectively plll::LatticeReduction::SVP_KannanSchnorrEuchner.

Schnorr's new SVP solver

A (single threaded) version of Schnorr's new SVP solver, as described in [19] by C.-P. Schnorr.

Schnorr's new SVP solver can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_SchnorrFast.

This implementation is still experimental.

Warning: This algorithm is not (yet) working well in high dimensions, and might be slow in medium dimensions.

Voronoi Cell computation

A deterministic SVP solver which first computes the voronoi cell of the lattice. While being deterministic and asymptotically faster than enumeration, in practice this algorithm is only usable for very low dimensions, say at most 10, where enumeration is still much faster. This algorithm was described by D. Micciancio and P. Voulgaris in [11].

The Voronoi Cell SVP solver can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_VoronoiCellSVP.

Warning: This algorithm is only practical in very low dimensions!

List Sieve

The probabilistic list sieve SVP solver. It was described by D. Micciancio and P. Voulgaris in Section 3.1 of [10].

The List Sieve SVP solver can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_ListSieve.

This implementation is still experimental.

Warning: This algorithm is not (yet) working well in high dimensions due to large memory consumption, and might be quite slow in medium dimensions.

List Sieve Birthday

The probabilistic list sieve (with birthday paradox exploitation) SVP solver. It was described by X. Pujol and D. Stehle in [14].

The List Sieve Birthday SVP solver can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_ListSieveBirthday.

This implementation is still experimental.

Warning: This algorithm is not (yet) working well in high dimensions due to large memory consumption, and might be quite slow in medium dimensions.

Gauss Sieve

The probabilistic Gauss sieve SVP solver. It was described by D. Micciancio and P. Voulgaris in Section 3.2 of [10]. Our implementation is similar to one by P. Voulgaris.

The Gauss sieve can be enabled by calling plll::LatticeReduction::setSVPMode() with the SVP mode plll::LatticeReduction::SVP_GaussSieve.

Warning: This algorithm is not (yet) working well in high dimensions due to large memory consumption.

Algorithm configuration

There are essentially two algorithmic configurations available for the lattice reduction algorithms:

different kind of Deep Insertions;
Simulated Annealing.

plll supports Schnorr-Euchner Deep Insertions as well as potential minimizing Deep Insertions. They are supported (directly and indirectly) by essentially all lattice reduction algorithms provided by plll.

The Simulated Annealing support is restricted to LLL and BKZ (classical and simplified). It is very experimental and should at the moment only be used for further experiments.

Deep Insertions

Classical LLL has two operations: size reduction, and swapping adjacent basis vectors to move a shorter vector more to the front. In [15], C.-P. Schnorr and M. Euchner not only describe BKZ, but also a modification to classic LLL which allows to insert basis vectors much more in the front if they fit somewhere earlier as well: the so-called Deep Insertions variant of LLL.

Another variant of Deep Insertions are potentially minimizing Deep Insertions, introduced by F. Fontein, M. Schneider and U. Wagner [3] [4]. This led to two algorithms PotLLL and PotLLL2 which are LLL with some kind of Deep Insertions which, opposed to the Schnorr-Euchner Deep Insertions, allow to still prove polynomial running time for the algorithm. For Schnorr-Euchner Deep Insertions, it is not known whether the algorithm has polynomial running time or not, although C.-P. Schnorr and M. Euchner claim this for restricted variants (without proof) in their original paper (Comment 2 at the end of Section 3 of [15]).

There are four different Deep Insertion methods, which can be set using the plll::LatticeReduction::setDeepInsertionMethod() function as the first parameter:

plll::LatticeReduction::DI_None: disables Deep Insertions; this is the default;
plll::LatticeReduction::DI_Classic: uses Schnorr-Euchner Deep Insertions;
plll::LatticeReduction::DI_MinimizePotential1: uses potential minimizing Deep Insertions as described in [3] and [4];
plll::LatticeReduction::DI_MinimizePotential2: uses a slightly different method for potential minimizing Deep Insertions as described in [4].

The second argument of plll::LatticeReduction::setDeepInsertionMethod() determines the Deep Insertions mode, which decides whether to do Deep Insertions before or/and after size reduction:

plll::LatticeReduction::DIM_BeforeSR: does Deep Insertions before size reduction;
plll::LatticeReduction::DIM_AfterSR: does Deep Insertions after size reduction;
plll::LatticeReduction::DIM_Both: does Deep Insertions both before and after size reduction; this is the default.

Note that for plll::LatticeReduction::DIM_Both, the Deep Insertion after the size reduction is only called if the size reduction did modify the basis. Also note that the mode can be set independently from the method via plll::LatticeReduction::setDeepInsertionMode().

Finally, it is possible to configure the range where vectors can be inserted by calling plll::LatticeReduction::setDeepInsertionChoice():

plll::LatticeReduction::DIC_First: if the second argument to plll::LatticeReduction::setDeepInsertionChoice() is t, then the current vector will only be tried to be inserted among the first t vectors of the base;
plll::LatticeReduction::DIC_Block: if the second argument to plll::LatticeReduction::setDeepInsertionChoice() is t, then the current vector will only be tried to be inserted among the (at most) t vectors before the current basis vector;
plll::LatticeReduction::DIC_FirstBlock: this is a combination of plll::LatticeReduction::DIC_First and plll::LatticeReduction::DIC_Block, i.e. the current basis vector can be inserted both at the beginning and in the block before the current vector;
plll::LatticeReduction::DIC_All: the current basis vector can be inserted at any position before itself; this is the default.

Note that the default setting, `plll::LatticeReduction::DIC_All, seems to yield exponential running time. Therefore, one usually chooses one of the other modes.

Currently it is not known which choices of Deep Insertions are particularly good; some research indicates that Deep Insertions can be as good as BKZ in some cases [6]. We are currently running experiments to provide guidelines which parameters to choose.

Simulated Annealing

Todo:: Write documentation for Simulated Annealing.

General configuration

Arithmetic

There are two arithmetics which can be configured: real arithmetic and integer arithmetic.

The real arithmetic is used for computing Gram-Schmidt orthogonalizations or duals of projected lattices. It can be set via plll::LatticeReduction::setArithmetic() and queried via plll::LatticeReduction::getArithmetic(). The following arithmetics are available:

plll::LatticeReduction::A_Rational: rational arithmetic with arbitrary precision integers. Will always return correct results, but is quite slow.
plll::LatticeReduction::A_Real: arbitrary precision floating point arithmetic. With a numerically stable Gram-Schmidt orthogonalization, it should always return quite correct results and be quite fast.
plll::LatticeReduction::A_Double: uses native double floating point arithmetic. Should be fine up to certain dimensions and very fast. Might result in hanging for too high versions.
plll::LatticeReduction::A_LongDouble: uses native long double floating point arithmetic. Should be fine up to certain dimensions and very fast. Might result in hanging for too high versions.
plll::LatticeReduction::A_DoubleDouble: uses double double floating point arithmetic which is obtained by representing a floating point numbers as the sum of two double values. Has higher precision then a double variable, but is slower and has no larger exponent range. Might not be available on every system.
plll::LatticeReduction::A_QuadDouble: uses quad double floating point arithmetic which is obtained by representing a floating point numbers as the sum of four double values. Has higher precision then double, long double and double double variables, but is slower and has no larger exponent range than double variables. Might not be available on every system.

Warning
While conversions between double double and quad double and some native types (int, float and double) are fully supported (by libqd), conversions to and from long double, long int, long long and the GMP and MPFR arbitrary precision types are not properly implemented (yet). So use on your own risk.

Todo:
Fully implement conversions between double double, quad double and long double, long int, long long and the GMP and MPFR arbitrary precision types.

Note that for arbitrary precision floating point arithmetic, i.e. for plll::LatticeReduction::A_Real, one can enforce a minimal precision by calling plll::LatticeReduction::ensurePrecision().

On the other hand, the integer arithmetic is used to represent the (integral) lattice's entries. It can be set via plll::LatticeReduction::setIntegers() and queried via plll::LatticeReduction::getIntegers(). There are two main different integer arithmetics:

plll::LatticeReduction::I_ArbitraryPrecision: uses arbitrary precision integers. They can represent any integer which fits into memory, and no overflow will occur. Slow, but always correct.
plll::LatticeReduction::I_LongInt: uses native long int integers. They can represent only a limited range of integers, and overflow might occur. Much faster, but only suitable for lattice bases with small entries.

There is a third option, plll::LatticeReduction::I_Auto, which tries to balance between the two above choices. It constantly monitors the size of the basis coefficients and switches between the two above arithmetics depending on the coefficient sizes.

The default choice is plll::LatticeReduction::I_Auto. Note that it can be slower than plll::LatticeReduction::I_ArbitraryPrecision!

Gram-Schmidt orthogonalization

plll provides a choice of several Gram-Schmidt orthogonalizations. The choice can be set with plll::LatticeReduction::setGramSchmidt() and queried with plll::LatticeReduction::getGramSchmidt().

plll::LatticeReduction::G_Classic: classical Gram-Schmidt orthogonalization. Uses formulae to update Gram-Schmidt coefficients on swaps, transformations etc., which can introduce additional error with floating point arithmetic.
plll::LatticeReduction::G_ClassicInteger: Integer-based Gram-Schmidt orthogonalization. Internally uses arbitrary precision integers respectively rational numbers. Slow, but always accurate.
plll::LatticeReduction::G_Givens: Uses Givens rotations to compute Gram-Schmidt orthogonalization. Only available for floating-point arithmetic (i.e. every arithmetic except plll::LatticeReduction::A_Rational). Uses formulae to update Gram-Schmidt coefficients on swaps, transformations etc., which can introduce additional error with floating point arithmetic.

Note that this is only available for floating point arithmetic, and not for rational arithmetic.
plll::LatticeReduction::G_NumStable: The default Gram-Schmidt orthogonalization. Uses numerically stable Gram-Schmidt orthogonalization as described by P. Q. Nguyen and D. Stehle in [12]. This arithmetic is more resilient against approximation errors than other approaches. Instead of updating Gram-Schmidt coefficients for swaps, transformations etc., these are recomputed to ensure maximal precision.

Note that some of the Gram-Schmidt orthogonalizations support spontaneous restarts (in case precision is too bad). This can be toggled via plll::LatticeReduction::setGramSchmidtRestart() and queried via plll::LatticeReduction::getGramSchmidtRestart(). This is only supported for plll::LatticeReduction::G_Classic and plll::LatticeReduction::G_Givens and currently still experimental.

Recording transformation matrices

It is possible to record all transformations done during lattice reduction in form of a transformation matrix. Assume that $b_1, \dots, b_k$ is the input system, and $\hat{b}_1, \dots, \hat{b}_\ell$ the output system.

For notational reasons, let us define two matrices. Let 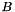$B$ be the matrix with 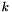$k$ rows having 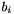$b_i$ as its 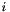$i$ -th row, and 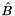$\hat{B}$ the matrix with 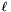$\ell$ rows having 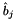$\hat{b}_j$ as its 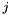$j$ -th row.

There are two transformation recording modes, which can be enabled by calling plll::LatticeReduction::enableTransform():

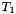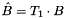plll::LatticeReduction::T_Normal: computes a transformation matrix such that $\hat{B} = T_1 \cdot B$ ;
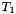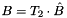plll::LatticeReduction::T_Inverse: computes a transformation matrix such that $B = T_2 \cdot \hat{B}$ .

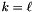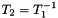In case $k = \ell$ , both transformation matrices are invertible and $T_2 = T_1^{-1}$ .

Note that $B$ represents the matrix at the point when plll::LatticeReduction::enableTransform() was called. A subsequent call, even with the same mode, resets the current transformation matrix to the identity matrix.

Transformation recording can be disabled by calling plll::LatticeReduction::disableTransform(). Its status can be queried by calling plll::LatticeReduction::isTransformationRecorded() and plll::LatticeReduction::getTransformationMode().

In case plll::LatticeReduction::isTransformationRecorded() returns true, the function plll::LatticeReduction::getTransformation() returns a non-NULL pointer to a matrix containing the transformation. In case plll::LatticeReduction::isTransformationRecorded() returns false, it returns NULL.

Callbacks

There exist several callback hooks in the plll library:

The most important hook is a callback function which is called in regular intervals from during the lattice reduction code. The default interval is approximately every 5 minutes (it can take longer when no lattice reduction code is executed, but for example an SVP solver).

The callback function can be set with plll::LatticeReduction::setCallbackFunction(). It accepts either one argument of type plll::LatticeReduction::CallbackFunction, one argument of type plll::LatticeReduction::CallbackFunction_LI, or two arguments of type plll::LatticeReduction::CallbackFunction and plll::LatticeReduction::CallbackFunction_LI. These are boost::function<> objects accepting a const reference to the current lattice basis and should return void. Please refer to the documentation of the function object types for more details on the function arguments.

Both currently set function objects can be obtained by calling plll::LatticeReduction::getCallbackFunction().

The interval can be set by calling plll::LatticeReduction::setCallbackInterval(); its argument is in seconds (as a double floating point number), and the default value is 60.0*5.0, i.e. 5 minutes. This is the minimal waiting time between two calls of the callback function.

Note that the callback function can throw an exception of type plll::LatticeReduction::stop_reduction to interrupt the reduction process. In that case, the reduction process will be stopped as fast as possible and control is handed back to the caller of the lattice reduction library.
The next most important hook is a callback function which will be called any time the code finds a newest shortest vector. For this, the (absolute) lengths of basis vectors will be compared all the time, which might add a small performance penalty. Usually it is negligible.

Such a callback function can be set with plll::LatticeReduction::setMinCallbackFunction(). It accepts either one argument of type plll::LatticeReduction::MinCallbackFunction, one argument of type plll::LatticeReduction::MinCallbackFunction_LI, or two arguments of type plll::LatticeReduction::MinCallbackFunction and plll::LatticeReduction::MinCallbackFunction_LI. These are boost::function<> objects accepting a const reference to the current lattice basis, an unsigned index into the lattice which indicates the currently shortest touched vector, and a const arithmetic::Integer & specifying its squared Euclidean norm. The return type should be void. Please refer to the documentation of the function object types for more details on the function arguments.

Both currently set function objects can be obtained by calling plll::LatticeReduction::getMinCallbackFunction().

Note that this callback function will not be called during enumerations (only at the end of the enumeration) or during processing of dual lattices.

Note that also this callback function can throw an exception of type plll::LatticeReduction::stop_reduction to interrupt the reduction process. In that case, the reduction process will be stopped as fast as possible and control is handed back to the caller of the lattice reduction library.
The third kind of hook are enumeration callback functions: they are called during enumeration (or other SVP solvers) when during this enumeration a new shortest vector (in the projected sublattice the enumeration is working on) is detected.

Such a callback function can be set with plll::LatticeReduction::setEnumCallbackFunction(). It accepts either one argument of type plll::LatticeReduction::EnumCallbackFunction, one argument of type plll::LatticeReduction::EnumCallbackFunction_LI, or two arguments of type plll::LatticeReduction::EnumCallbackFunction and plll::LatticeReduction::EnumCallbackFunction_LI. These are boost::function<> objects accepting a const reference to the current lattice basis, an int index specifying the first basis vector involved in the linear combination, as well as a row vector with integer coefficients which specifies the linear combination of the shortest vector. The return type should be void. Please refer to the documentation of the function object types for more details on the function arguments.

Both currently set function objects can be obtained by calling plll::LatticeReduction::getEnumCallbackFunction().

If the vector is vec and the int index is p, and the basis vectors (i.e. the rows of the matrix) are denoted by b[0], b[1], etc., then the vector found is
$\sum_{i=0}^{\text{\tt vec.size()} - 1} \text{\tt vec[}i\text{\tt ]} \cdot \text{\tt b[p} + i \text{]}.$

Note that this callback function will be only called during enumerations of primal lattices, not during enumeration of dual lattices.

Note that also this callback function can throw an exception of type plll::LatticeReduction::stop_reduction to interrupt the reduction process. In that case, both enumeration and the reduction process will be stopped as fast as possible and control is handed back to the caller of the lattice reduction library.

But it can also throw an exception of type plll::LatticeReduction::stop_enumeration to stop just enumeration. Then the so far shortest vector will be returned.

Note that in case of multi-threaded enumeration (Kannan-Schnorr-Euchner enumeration), it can happen that new shortest vectors are found during enumeration while the handler is already running in another thread. In such cases, the handler has to pay attention to this problem and make sure that no data races or (fatal) errors occur.

If for one of the three cases above, two callback functions are given, the better fitting one is selected depending on the currently used integer arithmetic (see Arithmetic). In case only one callback function is given, it is used for both integer arithmetics.

Warning: In case only one callback function is specified in one case, and the incorrect integer arithmetic is used, the arguments have to be converted for every function call. This can slow down execution a lot!

Verbose output

During operation, the library generates a lot of more and less informative messages. By default, the most important of these messages are written to std::cerr. By calling plll::LatticeReduction::setVerbose(), one can change the verbosity level (first argument) and optionally set a verbose callback function which can output the messages somewhere else, or simply store or ignore them.

The verbosity level can attain the following values:

plll::LatticeReduction::VOL_None: nothing is reported;
plll::LatticeReduction::VOL_Warnings: only warnings and errors are reported;
plll::LatticeReduction::VOL_Informative: informative messages, warnings and errors are reported;
plll::LatticeReduction::VOL_Full: everything is reported, including a lot of unnecessary and potentially annoying messages.

The current verbosity level can be queried by calling plll::LatticeReduction::getVerboseOutputLevel(), and the current verbose callback function can be queried by calling plll::LatticeReduction::getVerboseFunction().

Verbose callback functions accept a verbose level (for the current message) of type plll::LatticeReduction::VerboseLevel as the first argument, and a const std::string & with the message itself as the second argument. They return void.

The verbose level can have the following values:

plll::LatticeReduction::VL_Error: the message is a (fatal) error;
plll::LatticeReduction::VL_Warning: the message is a (non-fatal) warning;
plll::LatticeReduction::VL_Information: the message is purely informational;
plll::LatticeReduction::VL_Chatter: the message can be safely ignored. It can be helpful for debugging purposes or to see more about how the algorithms work.

Reduction Range

All reduction algorithms and SVP solvers can be restricted to a certain projected sublattice. If $b_1, \dots, b_k$ is the current generating system and a range of $[begin, end]$ is given, the lattice generated by

$\pi_{begin}(b_{begin}), \pi_{begin}(b_{begin+1}), \dots, \pi_{begin}(b_{end})$

is operated on.

The current range can be queried by calling plll::LatticeReduction::getRange(), and it can be set by calling plll::LatticeReduction::setRange(). If only one argument is given, this is taken as begin, while end is set to the maximum; otherwise, the input is of the form (begin, end).

Note that ranges can be modified if zero vectors are found (due to linear dependencies) and eliminated, or when new vectors are inserted (SVP solving without turning the result into a basis).

Multi-Threading

Parts of the plll library support active multi-threading. At the moment, this is limited to parallel enumeration (see Kannan-Schnorr-Euchner enumeration). To control the maximal number of threads for parallel enumeration, one can set this number by calling plll::LatticeReduction::setMaximalCoreUsage(). Setting it to 0 lets the system decide, which usually results in as many threads as the machine has (logical) cores.

The current number of parallel threads can be queried by calling plll::LatticeReduction::getMaximalCoreUsage(); the default value is 0.